What's In Hibachi Sauce

3: Boolean Algebra

There is a simple and effective way of analyzing the behavior of logic circuits known as Boolean algebra, in honor of its creator, the English mathematician George Boole (1815-1864) . Strictly speaking, when George Boole created Boolean algebra, it did not just with digital logic circuits in mind, because in his time not only had not been invented integrated circuits and transistors, even bulbs were expensive electronic enabled the development of radio. He was an engineer of our time, Claude Shannon (1916-2001), who came up with the idea that the principles of Boolean algebra I learned in college were very similar to the electrical circuit was studying. In fact we have been using since the introduction of the three basic logic functions. The functions OR, AND and NOT are expressions taken directly from the symbolic logic. What we do here is to formalize these concepts using symbols to represent binary words.

Boolean algebra is to use literal rather than combinations of "ones" and "zeros" for the analysis of logic circuits. We begin by considering the role NOT along with its truth table:

Here we temporarily waived because the triangle diagrams of logic circuits is bubble which represents the reversal of the entry. Note that the input is A and the output is C, and the output is called the negation of A (investment value), the effect is represented by a horizontal line placed over the symbol A.

Since the output is NOT always the logical inverse of the input A, we can represent the output of the NOT as

Output = A

thus placing the horizontal bar above to say that the output is the inverse or add input. This is read can be read in various ways such as the inverse of A, the complement of A ", or" refused ", all equivalent. In this book, if it has been possible, has become yet another thing for teaching purposes, is written the symbol of a variable color logically inverted blue . In addition, difficulties typographical symbols to represent a horizontal bar placed over them, in many books and many computer monitors with certain combinations operating systems and Internet browsers is preferable or even mandatory to resort to another type of representation through apostrophe ('). Under this representation, which has put an apostrophe on your right be taken as an inverted variable in Boolean sense. If the apostrophe is placed immediately to the right of a parenthetical expression, then entire expression in parentheses should be considered logically denied. All this means that in this book the following expressions must be taken as completely equivalent:

A = A '

A + B = (A + B)'

A • B = (A • B) '

ā = (a ')'

Whenever possible or convenient, when writing negated variables are used both systems of notation for the reader to become accustomed to using the two typing systems.

now consider the OR function with its truth table:

Note in the Table of Truth as the output of OR like the sum of the values \u200b\u200bto their inputs. For example, in the first line we have to zero (0 ) plus zero (0 ) is zero (0 ). In the second line we have to zero (0 ) plus one (1 ) is equal to one (1 ), and the third line we also have one (1 ) plus zero (0 ) is equal to one (1 ). Guided by this observation, we postulate that the output of the OR is equal to something we call logical sum of the values \u200b\u200bto their inputs, ie:

Output = A + B

Perhaps the reader will have noticed that, as we see in the fourth row of the table Indeed, one (1 ) plus one (1 ) is equal to one (1 ), ie:

1 + 1 = 1

This relationship may perplex many at first sight . This is when he warns the reader that one thing is logical sum of two variables, carried out a block OR, and quite another thing is the sum two binary variables. The logical sum or Boolean sum of and 1 equals 1 1, while the sum of binary 1 1 and is equal (in the binary numbering system) to 10 .

Regarding the latter we must remember that we are dealing with an algebra different from the classical algebra. We must therefore adapt our minds to the mathematical structures required for the study of logic circuits, it is the Boolean algebra not our classical algebra the "algebra" to understand the machines in their world of "on" or "ones" and "off" or "zeros". The discovery of this fact by Claude Shannon was what enabled the appropriate mathematical operation of logic circuits, which are so called because they are circuits whose behavior is described with the laws of symbolic logic (originally used for the study of human thought as such without any reference to electrical circuits) settled by George Boole.

We now consider the AND function with its truth table:

Note
Truth Table for C how the output of the AND resembles the product of the values \u200b\u200bto their inputs and A B . For example, in the first line we have to zero (0 ) by zero (0 ) is zero (0 ). In the second line we have to zero (0 ) one (1 ) remains equal to zero (0 ). In the third line we also have one (1 ) by zero (0 ) is zero (0 ). It is in the fourth row where we have one (1 ) one (1 ) is equal to one (1 ). Guided by this observation, we can ensure that the output of AND is the product of input values, namely: output

= A • B

In Boolean algebra, there are also a number of relatively easy to prove theorems (this is done in the solved problems section), which are:

(1) A + 1 = 1

(2) A • 1 = A

(3) A + 0 = 0

(4) A • 0 = 0

(5) A + A = A

(6) A • A = A

(7) ā = to

(8) A + A

= 1 (9) A • A = 0

Using the above results, we can analyze any logic circuit and, very often, simplify. For example, suppose a logic circuit has the following output:

AB + B + C + CD

The first step is to factor common terms as follows:

(A + 1) • B + C • (1 + D)

Using the first theorem given above, this reduces immediately to:

(1) • B + C • (1)

B + C

It is clear that it is easier and cheaper to build the circuit using the latter term (only requires a two-input OR) that using the original expression which requires two AND and OR blocks of four entries.

Previously, lacking the resources of Boolean algebra, the only way to discover the behavior of a logic circuit built from three basic logic functions was applied to the inputs all possible combinations of "ones" and "zeros" and track changes for each of these combinations along the circuit getting the outflow, and thus build a truth table. And there was no obvious way to simplify the circuit by reducing the number of components required for its construction. But now, with the use of Boolean algebra in our hands, instead of tracking along a logic circuit all possible combinations of "ones" and "zeros" up to the output of the circuit, we can trace the effect components on the symbolic variables entry, and without recourse to the "ones" and "zeros" can even try to do a simplification of the circuit before we were not enabled to do. Here is an example of how we can "track" inputs until the output of a logic circuit to obtain a symbolic expression for output in terms of input variables:

We can see in the DNA that is on the left side of the diagram, the input variables and B C are placed at the exit of it as BC, and this serves as one input to NOR at the top of the diagram, which sum (in the Boolean sense) BC to the other input A , taking place immediately following this logic to investment obtain the expression A + BC to the output of the NOR. On the other hand, the NAND which is located below this NOR receives as input to the signal that arrives from the terminal A with the signal that arrives from the terminal B previously processed by the inverter NOT, so that the two inputs to this NAND are A and B . The processes these two inputs NAND performing the multiplication first (in the sense Boolean) of these inputs to produce the term A B, which is immediately invested by the investment bubble of the NAND becoming the term shown in the diagram. Following the tracing of symbolic variables, we reached the final expression of Q output, which certainly seems to be an expression which may be simplified by Boolean algebra.

An important concept in our study is the concept of minterm , which allows us to obtain the output expression for a circuit from its truth table.

Consider a circuit whose truth table is as follows:

focus our attention on those outlets that have the value 1 . In this case, are the outputs ₂ f and f 3.

By definition, a minterm corresponding to the output of a circuit is the product of the literals A and B represent the input variables so that an outflow of 1 . In the second row of the Table of Truth, since A = 0 must invest to ensure that your product with B = 1 an outflow 1. Thus, we see that the first minterm is:

F ₂ = A B ___ [= A ' B]

Using the same reasoning, the second minterm is:

f ₃ = A B _____ [A B ']

We turn now to a fundamental theorem (the proof is not difficult but will not take place in this book for the benefit of mathematical demonstrations who is not his forte) that tells us the output of a logic circuit is equal to the sum the minterms of Truth Table.

Then, the output of the circuit in this case is:

Output = f 2 + f ₃

Output = A B + A B

Another important concept is the concept of maxterm .

Consider a logic circuit whose truth table is as follows:

now concentrate our attention on those outputs that are zero. In Here are the outputs f ₂ and f 4.

By definition, a maxterm corresponding to the output of a circuit is equal to the sum of literals A and B represent the input variables so that an outflow of 0 (compare the definition the minterm). In the second row of the Table of Truth, since B = 1 , invert the variable B to the sum with A = 0 produces an output of 0 . Thus, we see that the first maxterm is:

_{f 2 = A +} B

Using the same reasoning, the second maxterm be:

f ₄ = A + B

We turn now to another fundamental theorem of the theory of logic circuits tells us that the output of a logic circuit is the product of their maxterms Truth Table.

The output of logic circuit in this case is:

Output = f ₂ • f ₄

Output = ( A + B) • ( A + B )

We can remove the parentheses and simplify this expression to carry out the multiplications required in a similar way to how which are used in traditional algebra:

Output = A A + A B + A B + B B

According to one of the theorems listed above:

A • A = 0

and applying one of the theorems we have:

B • B = B

We then output reduces to

Output = A B + A B + B We

factor the first two terms as follows: Departure

= (A + A) • B + B

Using the theorem that tells us A + A = 1, the expression simplifies to Out

= B + B

But another theorem tells us that any variable coupled logic itself gives us the same variable (this theorem applies equally to all variables and In the case of inverted variables), that is the theorem:

A + A = A

Then the final expression reduces simply to:

Output = B

Then the circuit two inputs A and B represented by the Truth Table last all that does is reverse the entry B and ignore the input A. It is, in essence, simply an inverter connected to the logic signal B. A new inspection of the table confirms this truth at first we were not so obvious.

We, therefore, get the output expression for any logic circuit from its truth table through either minterms or through maxterms. The decision to use maxterms minterms or merely a matter of convenience. For example, if the truth table for a circuit that has fewer minterms maxterms, possibly using minterms is reached more quickly to a final expression.

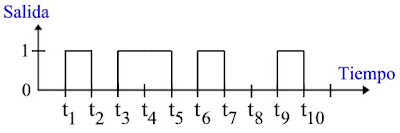
Finally, we will study the concept of timing diagram, which is always read from left to right .

Suppose that, over time, a logic circuit produces the following output in equally spaced times t _n :

During the time t _{1 at} 2, the output is 1 . During the time t at _{2 3} , the output is 0 . We can see over time t at 1 3 has formed the word:

10

During the time t _{3 4} at the output is 1 . And over time t at _{4 5} output is also 1 . We see that in the course of time t 1 at ₅ has formed the word:

1011

Thus, from the beginning of time t 1 until the end of time t ₁₀ has formed the word:

101101001

In general, given a timing diagram can be obtained from the same binary word it generates long as we are sure of the spacing of times between a "bit" and he continues . The precise division of time is crucial to establish and properly distinguish the "ones" and "zeros". In the case just to see if the division of time in a digital system timed out twice what we just saw, then instead of the word 1011 generated since the beginning of t ₁ until the end of t ₅ could well have had the word 11001111. And if the triple, then the word should have been 111000111111. This detail becomes much more important when the binary word that is being sent or processed is a word that consists of pure "ones" (as 11111111) or pure "zero" (as 00000000) because in that case same word does not give us absolutely no clue how many "bits" form.

Just as we can get a timing diagram of the binary word shown by the diagram, the same way given a binary word can be obtained from the same timing diagram that produces it. For example, the timing diagram of the word:

11011101

will be as follows:

Too often in the study and analysis of digital systems, timing diagrams diagrams are presented as multiple times, synchronized. This means that instead of a single plot can have two, three, or more diagrams, aligned one above the other so that their times each match. Below is a diagram multiple times a digital circuit that has four outputs instead of one, designated as Q ₀ , ₁ Q, Q 2 and 3 Q:

Although at first view is not enough, the circuit that produces this diagram multiple times is conducting very important work. We can understand better what is happening if settled outputs so that the binary word is formed:

_{Q 3 Q 2 Q 1 Q 0}

Now let us see what will is happening as time elapsing left to right, let the binary words which are formed starting from the first:

_{Q 3 Q 2 Q 1 Q 0} = 0000

_{Q 3 Q 2 Q 1 Q 0} = 0001

_{Q 3 Q} Q 2 ₁ Q ₀ = 0010

Q

_{3 Q 2 Q 1 Q 0 = 0011}

_{Q 3 Q} 2 1 Q Q ₀ = 0100

∙ ∙ ∙

may by now be obvious what is making the logic circuit that produces this timing diagram . Is a binary counter count up. is counting towards up in the language of electronic machines in the binary language of "ones" and "zeros".

The following is a timing diagram produced by a multiple binary counter countdown, which is a binary counter that is counting down , like a countdown:

The observant reader will have already realized that the logic circuit that produces this output timing diagram is complemented : Q ₀ , Q 1 , Q 2 and Q 3. In fact, if we compare this diagram with the previous times, we will soon realize that we can obtain a binary counter to count down (down ) of a binary counter to count up ( up ) with Just because some investors NOT connect to the outputs Q ₀ , ₁ Q, Q ₂ and Q 3 binary counter counting up .

then are shown in animated action several times diagrams for several of the basic logic functions have studied so far ( zoom in to see the special effects animation):

Consider first the diagrams times corresponding to the AND displayed on the first line in the left column. At the start of the animation, the two inputs to the AND have a " 0 " logical, thus leaving the DNA also has a value of "0 ." Over time, the top entry will change from " 0 " a " 1 ." But as is an AND block which requires both inputs are "1 " to produce an output of "1 , the timing diagram corresponding to the output remains at" 0 . " Shortly thereafter, the bottom entry is also set to "1 ", which both inputs are already " 1 ." This causes the output timing diagram of DNA change immediately " 1", and this change is confirmed by light-emitting diode LED to the change. After that, toward the upper input value of "1 " a " 0 ", the output of the AND also falls back to " 0 " what which is confirmed by the timing diagram at the output of AND and the indicator light.

In the same column, third row, we have an OR block, which will output " 1" when either input is "1 ." Following the action in the timing diagram as we did in the case of the AND, we can verify what we are saying the timing diagrams for the OR as a whole. In the second row of the same column have a NAND block and the fourth line we have a NOR block diagrams with their time. There

laboratory equipment, a bit expensive by the way, used precisely to obtain the diagrams circuit times as we have been studying, known as logic analyzers, which have a below

The following timing diagram, we have illustrated the behavior of a NAND with three input terminals A , B and C , and an output designated as And :

The way to read this timing diagram is as follows, proceeding always from left to right. At first, the three inputs A , B C and have a logical value of 0 , which output is And 1. As we left moving left to right, we see that the entry A is led to 1 0 , although this has no effect on output And because it is a NAND. Following this, and the entry A maintained at a value of 1 , entry B is also taken to a logical 1, but again, nothing happens to the output because it is a NAND . After that, the entry C is also taken to a logical 1, which the three inputs of NAND already have a value of 1 . This produces a transition in the output value of And 1 to 0 , which is highlighted by the line smitten. Finally, the entry A is carried back to value 0 it originally had, which produces a change almost immediately at the output of NAND And it takes a 0 1 . This concludes the reading of the timing diagram.

Note that in the last paragraph we use the word almost .

times diagrams described above are modeled based on the ideal timing diagram , which supposedly a signal instantly amounts of 0 to 1 or down instantly of 1 to 0 , which requires that a voltage (say, +5 volts) to rise instantly to a value from zero volts to the value of +5 volts without any time delay, or vice versa. In logic circuits built with real components such as semiconductors, resistors and capacitors, this quite simply is not possible, because to begin with no signal can propagate faster than the speed of light, and long before reaching come into play that limit other phenomena that impose restrictions regarding the speed with which you can perform a transition to 0 1 1 or of to 0 . The following two timing diagrams show what happens to a real signal, in addition to showing a common difference in the representation of the two major types of signals: (a) a signal representing a pulse , and (b) signal representing a binary data :

In the first diagram (a), we have a diagram of a real pulse, which does not rise instantly to a value of "0 " logic (which vertical scale to the left would represent a voltage of zero volts) to a value of "1 " logic (which in the vertical scale on the left would represent a voltage of something like +3 or +5 volts volts depending on the type of components used in the circuit). The signal takes to go from " 0 " to " 1 " time T r usually known in the literature as rise time (rise time ). And when the signal falls back to " 1 " a " 0 ", the signal takes time T f known to fall in the technical literature as downtime ( fall time). A signal as shown in this diagram, if repeated, identically repeated again and again, it could represent something like the pulses of a clock used to implement logic circuits known as a circuit sequential to be studied in later chapters of this book. In this case, the time interval between a pulse and he still is known as the period T clock signal, lasting from t 1 to 3 t . The mutual f T period, or f = 1 / T is the signal frequency . Anyone who has ever bought a desktop PC to disburse money from his own pocket without realizing perhaps already familiar with this concept, because this is the speed with which the computer can work, as is well known computers faster (and more desirable) are precisely the highest price. Thus, when we speak of a 500 MHz computer, we are really talking about a computer with a speed, or rather, with a pulse frequency of master clock domestic, 500 million cycles per second. And if speed is 2 GHz, the internal master clock of the computer is cycling at a rate of 2 million cycles per second.

In the second diagram (b), we have a timing diagram to represent a binary signal which can cause some confusion for neophytes who are not used to read it, because we have two data superimposed over each other. This diagram can be interpreted as a single signal with two alternatives where red line represents the alternative the signal goes from " 0 " a " 1 " at a time climb _{r t} , and where the blue line alternative is that the signal is going from " 1 " a " 0 " and in which case we are talking about a fall time t f . Thus, the red line represents a signal that short amount of " 0 " a " 1 " and after that it falls back to " 0 " while the blue line represents a signal that falls short of " 1 " a " 0 " and after that back up again " 0 " a " 1 ." These are both possible and acceptable behaviors that can be mixed binary signal shown by the diagram. However, this mixed binary signal also has another type of interpretation which does not interpret it as a single signal but as several signals being sent simultaneously . Under this mode of interpretation, a time chart with two lines "cross" in which the start of a cycle of operation is one of " 0 " a " 1 " while the other goes " 1 "a" 0 "both signals back to their original values \u200b\u200bat the end of the cycle is actually representing not a single line but several parallel lines that carry information simultaneously (such as home A ₆ A ₅ A ₄ A ₃ A ₂ A ₁ A ₀ ), some of which may have a logical value "0 " and others of which may have a logical value of "1 " at the same time.

As another example of mixed timing diagram like the one we have just seen, it is possible that the reader is in the technical literature something like the following:

A timing diagram of this type is one thing I find to be studying something like the chips (there are more details about this in the Supplement # 2 of this book, Microprocessor ). This timing diagram tells us that is generating a series of clock pulses (from a terminal called clock) and that after a first clock pulse can place binary information in a set of terminals designated address (address ) . Again, the line is divided into two may seem puzzling. However, there is some voltage "intermediate" between " 0 "and" 1 "(which, incidentally, is not permitted within the binary logic), which tells us that this diagram is valid time (valid ) with duration two-pulse "clock" ( clock) can put information that can consist of both "some" (1 ) and "zeros" ( 0 ) specifying an address (address ), after which or deposit can take over four cycles of "clock" parallel data into a set of designated terminal data (data ) which may consist of both "some" as "zeros".

As discussed in the section of solved problems related to this chapter, Boolean algebra is crucial to design digital circuits that are responsible for carrying out the binary sum (not the Boolean sum) of two different binary numbers A and B. The building blocks that serve as a starting point for this are the Middle Adder (Half Adder ), the Full Adder ( Full Adder), the Middle Subtractor (Half Subractor ) and Full Subtractor (Full Subtractor ). These building blocks allow us to perform arithmetic operations, and as the building blocks are identical, the use of a greater number of identical blocks allows us to greatly increase the numerical accuracy of arithmetic we can carry out such incredible precision to which digital computers owe their fame. One detail that had been pending since we introduced the binary numbering was the problem of carrying out arithmetic operations with binary numbers not only positive but also negative binary numbers , the discussion was postponed until now because in that introductory chapter We did not have the three basic logic functions and much less Boolean algebra which have already Now for the design of logic circuits, which is why it is time to revisit the issue.

In the first chapter of this book, by introducing the binary numbering, described a universal convention under which the negative binary numbers are distinguished from the positive with a "bit" since the beginning of the binary number, where the " 0 "represents a" + "and" 1 "represents a" - ". It was also noted there that if you try to add two binary numbers of different signs under this convention the arithmetic result will be incorrect. For binary arithmetic with different signs are usually use an alternate representation based on one-complement (in English: one's Complement or 1's Complement). Representation is known as the two-complement (in English: Two's Complement or 2's Complement ).

Before looking in depth into the matter on the sum of positive and negative numbers in binary, we will discuss here briefly about how to work a method known as the 9-snap in the decimal system. This method allows us to perform the arithmetic operation of subtraction (subtraction) between two numbers or whatever it is, the sum of a positive number a negative number (the number being subtracted). In the decimal system, the 9-snap of a number is obtained by replacing each digit of the least number of nine digits. Thus, the 9-complement of 147 is 852 and the complement of 605 is 394. Under 9-plug technique, to add 605 to -147 the procedure is as follows:

As can be seen, first obtained complement number whose sign is negative, add the numbers, and after this there is a 1 previously obtained from the operation of "Go" to what we have, so achieve the end result, which in this case is +458. Thus, the arithmetic operation of subtraction is reduced to an arithmetic operation. Instead of subtracting as we would in a calculation made by hand, change 147 by proceeding to add its complement. The overflow is taken to the column of "units" and added, obtaining the correct result of the operation. The following will take place the same operation, but reversing the signs:

Here we also take the complement of the negative number. In this case there is overflow, and the final procedure is somewhat different. The amount resulting from the positive number and complement the other number is just complemented, and the result is assigned a negative number.

The justification of why this method always works lead us to a discussion on the subject of the Rings and mathematical equivalence classes, which would divert us from our central objective without adding clarity to the art. We just know that this method never fails because it has a strong theoretical rationale.

As in the decimal numbering is the method of 9-snap to add a positive number and a negative number in other number systems there is a similar procedure supported by the same reasons theoretical mathematics. In our case, we are interested in applying the technique to the binary system, the language of "ones" and "zeros" which is what the machine understands. That said, all this better prepared to define what is "a complement" in the binary system. This representation we simply take the logical inverse of the binary number, or whatever it is, its complement (here comes the designation). Thus the one-complement the binary number 00000010 (equivalent to the decimal number 2) is 11111101.

Under the representation of the "two's complement" take first the 1-complement the number in the manner stated above, simply by investing course. After that, you add 1. This results in consolidation of the number in 2-complement . It is important to emphasize that taking a positive number to represent the procedure as 2-add it automatically becomes a negative number.

Let's look at an example of how we obtain the representation of the number -9 under the scheme of 2-complement binary using a four-word "bits" (a nibble ) with the first bit reserved for the sign of number and the three remaining bits reserved for the magnitude of the number. We start with the binary equivalent of decimal number "9", which is " 01001." We now apply the investment process logic to get the 1-complement, which is " 10110." Finally we add 1 and get " 10111." This is the equivalent to 2-complement , negative number -9.

Given a number 2-complement, we can convert a negative decimal form by adding the "powers of 2" bits "1", but giving a "weight" negative bit (the sign) is more significant than left. For example: 11111011

2 = - 128 + 64 + 32 + 16 + 8 + 0 + 2 + 1 11111011

2 = - 5

or for example: 10001010

2 = - 128 + 0 + 0 + 0 + 8 + 0 + 2 + 0

_{2 10001010 = 10001010 = -118}

For these conversions are clear, we will use another simple example by first converting the number 13 in decimal to negative using its representation as 2-complement, and then using this result we get the negative number expressed in decimal. The number 13 in binary is 00001101 . If we reverse the bits get as 1-complement 11110010. Now we add 1 , and obtain the 2-complement 11110011. We check the response becoming 2-add this number to its decimal equivalent: 11110011

= -128 + 64 + 32 + 16 + 0 + 0 + 2 + 1

11110011 = -13

Notably
that 2-complement of zero is zero: the first inversion gives us a string of "ones" and add "1" This changes all the "ones" back to zero. When performing this operation, overflow is simply ignored.

Next A table that shows the equivalent of several positive and negative decimal integers represented in the second column under the "magnitude sign (the first bit is used for the sign and the three remaining bits of magnitude) and represented the third column under the 2-complement scheme :

The same information may be easier to visualize and remember the following "binary cycle"

We now have out the sum of two numbers of different signs, +2 and -3, in the 2-complement representation, using an extension one byte (eight bits). Since the only number that carries a negative sign is 3, 3 of which take the binary equivalent (positive) is 0011, it logically invest to get the 1-complement, which is 1100, and we add 1 thus we get to 2-complement negative number -3, which can add directly (in short binary Boolean sum not!) the +2 positive number for " 11111111, which is equivalent 2-complement of the number -1 (in 8 bits).

The result of the arithmetic operation is given as see, in 2-complement, and is a negative number. Notice how this time yes we got the results correct arithmetic.

for the proceedings to be clear, we do a second operation using 5 bits, adding the numbers +13 and -9. At number 13, being positive, we leave as is, its binary equivalent is 01101. The number 9, being negative, should be converted to its representation as a 2-complement . The binary equivalent of 9 is 01001 , its 1-complement is 10110, and its 2-complement is 10111. If we add and 1 01101 0110 , get 00100, or +4, which is the correct result according to the original signs, the response also having the correct sign.

There are thus three types of arithmetic involving signs: (1) the addition of two positive numbers, (2) adding a positive and a negative number, or whatever it is, a subtraction operation, and (3 ) the addition of three negative numbers, and the method 2-complement work in the three cases summarized as the following three examples:

The advantage of using the representation of 2-complement is you do not have to worry about by the sign bit to perform arithmetic operations of addition and subtraction; the end result will always be correct regardless of the signs of the numbers. Not having to be explicitly testing the sign of the binary numbers to perform arithmetic operations can result in a substantial improvement in speed when such operations are carried out by logic circuits.

only remains to make a final warning regarding the use of the symbol "=" (equal) in the Boolean algebra. This symbol tells us that two expressions connected by it, for example:

are equivalent Boolean algebra (both produce the same truth table) but not the same the concept of common use in classical algebra.

This means that the following are valid in the classical algebra :

are incorrect in Boolean algebra. Indeed, given an expression in Boolean algebra, we can simplify it using the theorems seen above, relating each new expression with the previous symbol using the equivalence "=". However, as shown above simplifications are devoid of any meaning in algebra Boleana.