Problem: Write a normal count of 20 objects using the base 4 number system.
Problem : How much is the decimal number 13 in base 6 number system?
The number 13 in decimal is the number 21 in base 6 system. Symbolically:
13 10 = 21 6
Problem: Convert the number 20 to base 4 system using the method of successive division.
Applying the method of successive division, we have:
The equivalence of the decimal number 20 to the corresponding 1104 in base 4 system can be represented as follows:
20 10 = 110 4
Note how to convert decimal number 20 to number 110 in base 4 system, we divide the number first (20) between the base (4) highlighting the first residue (0). The ratio of the first division (5) is again split between the base (4) adding adding the remainder of the second division (1) the residue of the first (0) to be shaping the issue. Since the second ratio (1) and can not be divided by 4, with the second ratio (1), the second residue (1) and the first residue (0) form the number 110 in base 4 number system. Problem
: Convert the number 19 to base 2 system using the method of successive division .
proceed the same way as in the previous problem:
Symbolically, we express the result as follows:
19 10 = 10011 2
problem: Convert the number 49 to base 3 system using the method of successive division and check the result by a table .
Symbolically, we express the result as follows:
49 10 = 1211 3
The complete table of equivalencies to reach the desired number, which has been highlighted in cyan Ascendant numbering decimal system is as follows:
is obviously much more comfortable even for fairly small numbers resort to the method of successive division to try to reach an equivalent in a numerical basis by constructing a table.
PROBLEM: Transformanndo decimal numbers 13 and 25 in its binary equivalent, add these numbers both in decimal and in binary, putting both resolutions next to each other in order to compare the similarities. After that, convert the binary response to its decimal equivalent using the table of powers of 2 to check the response of binary addition.
First take out the "decomposition" of the numbers 13 and 25 in the equivalent base 2 system:
then will be out the sum of the decimal numbers 13 and 25, together with the binary sum of the numbers 1101 and 11001:
The decimal sum, to add 25 and 13 in the manner in which we are accustomed , garnering a response from right to left, first say "5 plus 3 equals 8. In this case, as the partial sum does not exceed 10, not "we" a unit to be added to the tens. The next digit, we get saying "2 plus 1 equals 3." With this, we have the result shown above, which is 38. Let's see how it carried out the binary sum . To perform binary addition, we proceed in exactly the same way, starting from left to right say " a more equals a 10 " (remember that in the binary system, there is a symbol for the number 2). We note the zero down (as in yellow) and say "we scored zero and we a ." In the next column of digits, proceeding from left to right as well as we do in the decimal system, we say "zero more zero equals zero plus a we wore equals one. " We write this one to the left of zero had written earlier, with which we already have a cumulative result of "10" in yellow, proceeding to the next column of digits in where we say "zero more a equals one , and we did not have anything like the addition above, we scored it a . " We already have a cumulative response of "110." We go to the next column of digits in which we say: " a more equals a 10 , and as we did not have any of the previous addition, we scored and we zero one." Our cumulative response reads as "0110". Thus we come to the last column to the left, where we have only the "1" which we say "we have a plus a we brought from the previous addition is equal to 10 , and as there are no more digits to add, we note that 10 to conclude binary addition. " Thus, the result of the binary sum is equal to the binary number: 100110
To check our answer, the decimal equivalent of this number according to the table of powers of 2 turns out to be: 100110
2 = ( 1) 2 5 + ( 0 ) 2 4 + ( 0 ) 2 3 + (1 ) 2 2 + ( 1) 2 1 + ( 0) 2 0
100110 2 = 32 +0 + 0 + 4 + 2 + 0
100110 2 = 38 10
100110 2 = 32 +0 + 0 + 4 + 2 + 0
100110 2 = 38 10
PROBLEM: Add the four numbers whose binary hexadecimal representations are 25h, 62h, and 52h 3Fh .
The four hexadecimal numbers, converted to binary representation, are:
25h = 0010 0101 = 62h
0110 0010 0011 1111
3Fh = 52h = 0101 0010
0110 0010 0011 1111
3Fh = 52h = 0101 0010
The sum of these four numbers shown below:
The result of the sum, 100011000 , also can be represented as its hexadecimal equivalent h 118 .
PROBLEM: Multiply the numbers 13 and 25 each in symbolism converting binary, binary numbers obtained by multiplying, and carrying out the conversion from the result to decimal symbolism.
The binary equivalent of decimal numbers 13 and 25 and were obtained in the previous problem, proving to be 1101 and 11001. With this, we carry out multiplication in a similar way as is done in the decimal system to which we are accustomed:
Note that conducting a purely binary multiplication is much easier than it seems to be first sight, since in fact only required to be carried out by multiplying successive additions according to the value that has each of the binary digit number that is chosen as a multiplier. If we increase the capacity of bits, we may be undertaking a range of really big numbers without much intellectual investment that we've done, and this multiplication is carried out at a speed electronics. Not for nothing more than a century, human inventors worked to build machines that could perform arithmetic operations such remarkable speeds!
Since the product of decimal numbers 13 and 25 is the number 325, we can check our answer obtained by converting the binary number to its decimal equivalent, which must also be 325. The procedure for this is shown below: 101000101
2 = ( 1 ) 2 8 + ( 0 ) 2 7 + (1 ) 2 6 + ( 0) 2 5 + ( 0 ) 2 4 + ( 0 ) 2 3 + (1 ) 2 2 + ( 0 ) 2 1 + (1 ) 2 0
101000101 2 = 256 + 64 + 0 + 0 + 0 + 0 + 4 + 0 + 1
2 101000101 = 325 10
101000101 2 = 256 + 64 + 0 + 0 + 0 + 0 + 4 + 0 + 1
2 101000101 = 325 10
PROBLEM: represent in BCD system the following numbers:
A) 50 123The BCD representation system of numbers indicated below:
B) 37
C) 4856
D) 102
E) 3971
F) 74
G) 95 437
PROBLEM: A microcomputer has a capacity of 16 bits. What is the largest number that can be represented in this capacity in the same:
A) using the binary system, and
B) by using the BCD system? compare the difference between the two cases .
A) Using the binary system, the largest number that can be represented with 16 bits is: 1111111111111111
This binary number equivalent to decimal number:
2 16 - 1 = 65.536 65.535 = -1
B) using the BCD system, the largest number that can be represented with 16 bits is:
1001 1001 __ __ 1001 1001 __
9 _____ _____ 9 _____ 9 9
9 _____ _____ 9 _____ 9 9
is, the number 9.999.
By using the BCD system instead of the binary system, we have a difference of 65.535 to 9.999 = 55.536. At other times when the costs to represent each digit was measured in terms of electronic and electromechanical relays bulbs instead of the tens of thousands of transistors microminiaturized we have today, this was considered a lamentable loss of capacity. Anyway, in our times there are many situations in which the use of the BCD is a need to provide more "human" that is understandable to ordinary people, whether on digital clocks, digital album art in ovens microwave, and digital multimeters used by technicians to measure voltages and currents. In these situations, the use of pure binary data would be almost indecipherable to humans, even the "natural language" of digital electronics.
PROBLEM: .10101 Convert the binary number to its equivalent in decimal.
Using the table of equivalence described in the text, we have:
.10101 = .10000 + .00100 + .00001
.10101 = 1 / 2 + 1 / 8 + 1 / 32
.10101 = 5 + 125 + 03 125
.10101 .65625 2 = 10
.10101 = 1 / 2 + 1 / 8 + 1 / 32
.10101 = 5 + 125 + 03 125
.10101 .65625 2 = 10
But we can get the same result as the other alternative, which is to express the binary number as a fraction of two binary integers after which he became both the numerator and denominator to an equivalent decimal and finally perform the division:
10 101 = 10101/100000
.10101 = (10000 + 100 + 1) / 100000
.10101 = (16 + 4 + 1) / 32
. 10 101 = 21/32
.10101 .65625 2 = 10
confirming the results obtained previously.
PROBLEM: 110,011 Convert the number from binary to decimal system.
To convert this binary number "mixed" having an integer part and a fractional part, just give each "1" binary value that corresponds to:
110 011 = 100 + 10 + 01 + 001
110,011 = 4 + 2 + 1 / 10 + 1 / 100
110,011 = 4 + 2 + 1 / 4 + 1 / 8
110,011 = 6 + .25 + .125
110,011 2 = 6,375 10
110,011 = 4 + 2 + 1 / 10 + 1 / 100
110,011 = 4 + 2 + 1 / 4 + 1 / 8
110,011 = 6 + .25 + .125
110,011 2 = 6,375 10
In the alternative form of solution, we express the number as a fraction of two binary integers after which converted both the numerator and denominator to its decimal equivalent performing the division:
110,011 = 110011/1000 = (100000 + 10000 + 10 + 11) / 1000
110011 = (32 +16 + 2 + 1) / 8
110 011 = 51 / 8
2 = 110011 6375 10
confirming 110011 = (32 +16 + 2 + 1) / 8
110 011 = 51 / 8
2 = 110011 6375 10
and the results obtained previously.
PROBLEM: Convert the following binary fractions to decimal equivalent, results were expressed as rational numbers (the ratio of two integers):
a) 011
b) .111
c) 1001
d) 1101
e) 10 001
f) 11 001
a) Using the conversion table, and proceed the same way in all cases:
.011 = .01 + .001 = 1 / 4 + 1 / 8 = 2 / 8 + 1 / 8 = 3 / 8
b)
.111 = .1 + .01 + .001 = 1 / 2 + 1 / 4 + 1 / 8 = 4 / 8 + 2 / 8 + 1 / 8 = 7 / 8
c) .1001
= .1 + .0001 = 1 / 2 + 1 / 16 = 8 / 16 + 1 / 16 = 9 / 16
d)
.1101 = .1 + .01 + .0001 = 1 / 2 + 1 / 4 + 1 / 16 = 8 / 16 + 4 / 16 + 1 / 16 = 13/16
e)
.10001 = .1 + .00001 = 1 / 2 + 1 / 32 = 16/32 + 1 / 32 = 17/32
f)
.11001 = .1 + .01 + .00001 = 1 / 2 + 1 / 4 + 1 / 32 = 16/32 + 8 / 32 + 1 / 32 = 25/32
PROBLEM: Represent the following decimal numbers to its binary equivalent, where necessary rounding to three significant figures.
a) 2 / 3
b) fifth
c) 15/16
a) First we out the division to make the number expressed as a decimal broken to:
2 / 3 = 0.6666666666 ...
Then we round the result to three significant figures:
2 / 3 = 667
To find the binary equivalent of the decimal fraction, we can carry out a sequence of successive subtractions referring to the table of equivalences which gives us the following series of steps:
.667-5 = 167 (A binary digit is equivalent .5 = 1 / 2 = .10000)
.167 to .125 = 042 (One digit is the binary equivalent of 125 = 00 100)
.042 - 03,125 = 01,075 (A digit binary equivalent is 03,125 = 00,001)
Consider well what you just made, referring to the table of equivalences we find that the fractional decimal number that corresponds directly with an exact binary equivalent that is the biggest of them all without exceeding the decimal number 667 is the number equivalent to .1 .5 binary. Noting this as a partial result and after carrying out the remainder of .5 decimal number 667, we have the number .167, which again consulted the table of equivalence to find the fractional decimal number that corresponds directly with exact binary equivalent is the largest all without exceeding the decimal number 167, which happens to be the number 0.125 is equivalent to 001 binary, noting this as a partial result. The answer is given by the sum of the partial results. This mechanical process can be repeated as often as we, approaching ever more closely to the original fractional decimal number.
So, the answer (about) is:
.10000 + .00100 + .00001 = .10101
b) 1 / 5 = 20
.2 to 125 = 075 (A digit equivalent binary is 125 = 00 100)
.075-0625 = 0125 (A binary digit is equivalent 00,010)
Since .03125 .0125 exceeds that, we can not subtract it from 0125, which we know that the next significant digit in the accumulation of partial results should be a "0." So the answer (about) should be:
.00100 + .00010 + .00000 = .00110
c) 15/16 = 938 (rounded to three significant figures)
.938-5 = 438 (A binary digit is equivalent .5 = 1 / 2 = .10000)
.438-25 = 188 (A digit binary equivalent is 25 = 01 000)
.188 to .125 = .063 (A digit binary equivalent is 125 = 00 100)
.063-0625 = 0005 (A digit equivalent binary is 0625 = 00 010)
The approximate answer is then:
.100000 + .01000 + .00100 + .00010 = .11110
PROBLEM: the following symbols Convert binary octal representation.
a) 10,110
b) 11 110
c) 11 011
d) 110 011
e) 111 000
f) 100 011
g) h
11,110,000) 11,001,100
i) 10,101,010
The solution procedure is straightforward, consisting of separate binary numbers in groups of three to do so from right to left:
a) 10110 = 10 110 = 26
b) 11110 = 11 110 = 36
c) 11 011 = 11 011 = 33
d) 110011 = 110 011 = 63
e) 111000 = 111 000 = 70
f) 100011 = 100 011 = 43
g) 11110000 = 11 110 000 = 360
h) 11001100 = 11 001 100 = 314
i ) 10101010 = 10101010 = 252
PROBLEM: multiply octal numbers 56 and 45, without leaving for anything in the octal system.
order to carry out the multiplication in the octal system, in which there is a symbol for our number "8", it should construct a "multiplication table" octal, which can easily be constructed by listing in count up all octal numbers from the one in front, and after that to jump to that list two at once, two by two to three times, two by two four times, two by two five times, and so on, and after that three at once, three at twice, three at three times, three by three four times, and so on, to be filling the boxes of the multiplication table of two by two, two and three, two by four, and so on. three for two, three by three, three four, etc., and so on, until you have the entire table, which turns out to be:
With octal multiplication table at hand, and bearing in mind the way in which it must carry octal out a sum, taking the smaller number (45) as the multiplier and the largest number (56) as the multiplicand as is customary in the usual multiplication, the operation procedure is as follows:
PROBLEM: Convert the following hexadecimal numbers to their equivalent octal system.
a) 3A7
b h) h 41FB
c) h 7C2E
d) D589A h
e) B0Ce5
h f) h
6FF23 Possibly the most
perform quick conversion is to directly convert each number to its binary equivalent hexadecimal (base-2) and after this grouping the binary digits in groups of threes (from right to left) after it carried out the conversion of each group octal system.
a) 3A7 h = 0011 1010 0111 2 = 001 110 100 111 = 1647 8
b) h = 41FB 0100 0001 1111 1011 2 = 0 100 000 111 111 011 = 40773 8
c) h = 7C2E 1100 0010 1110 0111 2 = 0 111 110 000 101 110 = 76056 8
d) D589A h = 1101 0101 1000 1001 1010 2 = 11 010 101 100 010 011 010 = 3,254,232 8
e) B0CE5 h = 1011 0000 1100 1110 0101 2 = 10 110 000 110 011 100 101 = 2606345 8
f) 6FF23 h = 0110 1111 1111 0010 0011 2 = 01 101 111 111 100 100 011 = 1577443 8







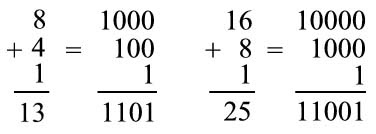






0 comments:
Post a Comment