PROBLEM: Determine the output produced by the following circuits shown binary inputs.
(a) start with the first two-input AND fed binary words and 10011001 10100101 . The analysis should be conducted bit-by-bit . Assume that the binary signals are entered from left to right, although for the purposes of this problem the input order of words is irrelevant. On the far right of both words have a binary bit "1 " in the upper terminal at the same time entering a bit " 1 " entering the bottom end. As a block AND, the resulting output for the first combination of bits is a " 1 ." Then enter the block AND the bits "0 " and " 0 ", which will produce an output of "0 ." With this, we formed and a cumulative output of "10 ." After this, go into the two terminals, respectively, the bits "0 " and " 1 ", which will produce the output AND a " 0 " with which the binary word output is already " 100 ." Continuing in this way, bit-by-bit, will the output of the AND is the result shown in the following table:
The word at the output of the AND of two inputs to the two binary words is then given 10000001.
(b) Proceeding in the same way for the two-input OR block, bit-by-bit , we can build the following table:
The binary word to the output of OR will 10111101.
(c) For the three-input AND block, we extend the definition of two-input AND, saying that the output of three-input AND is " 1 " only when all three entries with a value of "1 ." With this, proceed with the analysis bit-by-bit , we can produce the following table:
The binary word to the output of three-input AND is 00010000 .
(d) OR block For three innings, we extend the definition of two-input OR, stating that the output of the OR of three inputs will be " 1" when any of its three inputs have a value of " 1. With this, proceed with the analysis bit-by-bit , we can produce the following table:
The binary word to the output of three-input OR will 11111011.
(e) For NAND, we can carry out the analysis, bit-by-bit, taking into account first the initial action of the DNA of two bits from its input, and carried out immediately after this process logical negation as specified in the investment bubble placed at the exit of DNA with which it is transformed into a NAND. The first two bits in the input are " 0 " and " 1 " which by the action of DNA are converted into a " 0 " which by the action of the investment bubble is converted into a " 1 " final result. After this, the following two-bit input are " 1 " and " 0 ", which again by the action of DNA are converted into a " 0 " which by the action of the investment bubble is become a " 0 ." Proceeding in this way, we can build the following table, in which the result "intermediate", the binary word formed by the action of DNA before carrying out the action investment has been put in red:
The binary word to the output of NAND will 111110100.
PROBLEM: Is the following circuits useful for information processing?
(A) As this circuit has one input terminal, you can only put a "1 " or "0 ." Analyzing the first circuit by putting the binary word "10 " his entry, which contains the two possible combinations, we have:
The binary word "10 " to the input of NOT is converted into the binary word " 01 " to the output of NOT. Upon entering the binary words " 10 " and " 01 "to the OR, the output of this will be the binary word" 11 . "Because no matter what information you enter on entry, either a" 1 "or" 0 "the output will always be " 1 " concluded that this circuit can not process information.
(B) As in the previous case, as this circuit has one input terminal, only you can give the entry a "1 " or "0 ." Analysing the second circuit to the binary word "10 " on entry, which contains all possible combinations, we have the following:
Again, the binary word "10 " a NOT input is converted into the binary word " 01 " to the output of NOT. And entering the binary words " 10 " and " 01 " to AND, the output of this will be the binary word "00 ." Because no matter what information you enter on entry, either a "1 " or "0 , the output will always be" 0 "concluded that this circuit can not process information.
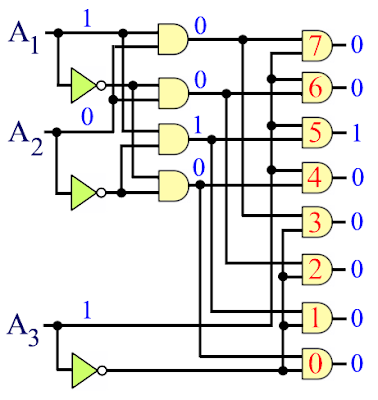
PROBLEM: Analyze the following circuit building a Truth Table the same. Note how the diagram is the signal flow path to the binary input word A 3 A 2 A 1 = 101.
We can see the circuit diagram with the word A 3 A 2 A 1 = 101 AND output only 5 will be activated a "1 ." The output of each of the remaining DNA will be disabled with a "0 ."
Next, we introduce a word different binary input circuit. Testing the combination A 3 A 2 A 1 = 001 and tracing the signal flow in the same way it was drawn to the combination A 3 A 2 A 1 = 101, we now find that only the output of AND 1 is activated with a "1 , being out in each of the remaining AND" 0 . "
Following the same procedure for each of the possible combinations of ones and zeros at the entrance A 3 A 2 A 1, we can construct the following truth table:
According to the Table of Truth obtained for each possible combination of ones and zeros to the input circuit will be activated the output of a single DNA in particular. The fact that every possible combination of ones and zeros to the input select only one of the AND output at the same time we can tell which is the binary word at the entrance. For example, we connect the output of each DNA to a numerical LED still in the recent past could have been an electronic tube type "Nixie"
which is now almost obsolete, having been replaced by light emitting diodes LEDs. The connection to different numbers still direct as follows:
Thus, by applying a combination of ones and zeros to the input of the circuit (for example, the word A 3 A 2 A 1 = 101, which equals the decimal number 5), LED lights inside the selected numeral corresponding to that combination (in this case, the numeral 5) . We, Therefore, a configuration that gives us information decimal to binary output to apply information to their entry. In other words, by introducing a binary number like "101 " read "5" in our decimal system to the output of the configuration. The setting is actually "translating" information converting it to binary decimal information. Circuits of this type are called decoder, and its function is to translate (or more appropriately, decode) binary information for subsequent use or for reading in decimal of the binary information. Generally, any circuit that produces a single output for each combination of ones and zeros on entry is considered as a decoder. Generally, a decoder, the trend is that more output terminals to the input terminals.
decoder shown above we would not be very useful in practice as only we can provide the number 7 digits to decimal. This can be remedied by adding to the decoder an AND and NOT, with two additional lines necessary for the decimal digit "8" and "9" can be started with binary input words A 4 A 3 A 2 A 1 = 1000 and A 4 A 3 A 2 A 1 = 1001 respectively. We would then have a binary decoder BCD to decimal. But there is a more economical and efficient alternative to reinvent the wheel: we seek to market a decoder chip that can perform precisely this task. An integrated circuit as the 4028 :
This integrated circuit works as follows: BCD binary number is put in the terminal "pin" input from 10 to 13, with the least significant bit (LSB) or bit "A" position in the terminal 10, and the most significant bit (MSB) and bit "D" as in the terminal 11. This decoder works exactly the same way as the one described in this problem, except that accommodates nine digits. If the entry is placed DCBA = 0101, the terminal "pin" 6 (which corresponds to the decimal number 5) will light up " 1" while all other output terminals will remain in " 0 " . If the integrated circuit puts a binary number greater than the decimal equivalent of 9, then all outputs will remain at "zero" any of the ten outputs come on.
If we use the binary decoder BCD a numerical indicators cover made from light emitting diodes LED seven segment, we go a step further by using an integrated circuit as the 4056 :
In this IC, BCD entries are in Terminals 2, 3, 4 and 5, and outputs which are connected directly to each of the seven-segment LED numeric display are made from the terminal 9 through 15. Alternatively, the integrated circuit 4056 is the latest 4511:
This decoder 4511 is capable of storing the BCD number as at the entrance, holding it in its internal memory until you enter another number BCD. For the integrated circuit "remembers" the binary number as your login, you must enable Terminal 5 ( latch enable) with a "1 ." (The records identified in the diagram of the circuit as "latches" are nothing more than four memory elements known as D flip-flops "to be studied in a later chapter, used for storage of each of the four bits of the BCD word.) Terminal of money laundering 4 ( blanking input), which is supplemented, usually has a " 1 " put into it, if we want all segments of the LED lights go off then put a " 0 " in this terminal. The terminal 3 ( lamp test), which is also supplemented, usually has a " 1 " put into it, if we want all seven-segment LED indicator lights light up regardless of the word that is stored in BCD the integrated circuit then put a " 0 " in this terminal.
All integrated circuits are discussed in this issue belong to the family of logic circuits manufactured with technology CMOS.
PROBLEM: We want to build a seven-segment LED made of light-emitting diodes (LED) red as shown in the figure below:
which entered in decimal form the binary number is applied to decoder logic which will convert the binary number in the appropriate power segments. Construct the truth table of decoder required whereas a voltage pulse to the LED lights and the absence of the switch them off.
Identifying the voltage pulse with a 1 and absence by a 0, then we have the following truth table:
Note that for a 4-bit binary word, there are six states (the last six in the truth table) which can not be represented in the light by its nature. These states are called redundancy. In order to properly decode a binary number such large segments, convert the binary number to the equivalent pure BCD system, which can be directly used indicators such segments based on LEDs.
The following cartoon, the light we have the numerical and below it the word binary BCD it is supplied, count up, with the binary sequence increasing in magnitude from right to left ( zoom to see the animated action in case the browser will not display it on the page):
PROBLEM: design has the following circuit as a decoder. Check if the statement is false or true .
The first step in solving this problem is to build a truth table for the circuit shown. It is not difficult to verify, for example, for entry A 2 A 1 = 01 only X output will be activated with a "1 ." Similarly, tracing the signal flow for all possible combinations of ones and zeros to the input of the circuit, we have the following truth table:
Since for the combination of ones and zeros to entry, only one output terminal is activated at the same time, we conclude that the circuit is actually a decoder.
PROBLEM: Analyze the following circuit constructing a truth table for it. Only one entry may be active at a time .
the truth table for this circuit is as follows:
can be seen in the Table of Truth that the circuit "becomes" the decimal numbers in the terminal input to the equivalent binary system output terminals. Circuits of this type are called encoder (encoder ), and its function is the opposite of the decoder.
this circuit applications are endless. Each terminal, for example, can represent a numeric key of an electronic calculator, with which information can be introduced in a binary calculator for subsequent processing.
PROBLEM: The next unit, commonly known as unit multiplex (MUX) allows only the output of one of the four channels of input. The desired channel is selected using the binary word A 1 A 0 as selector. What is the internal configuration?
The internal configuration should be something like what is shown below:
MUX block as follows:
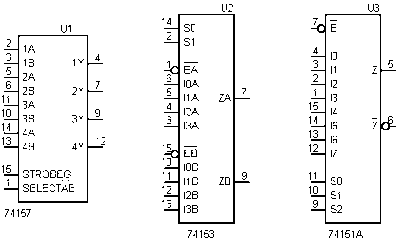
MUX unit is also known as Data Selector (in English, Data Selector.) The Data Selector is specified by output (or outputs) available from a number No entries. In the event that we have seen, we have a Data Selector 1-for-4 , because at any given time you can select one of the four inputs to be channeled out through the line ( Output .) There are several types of commercially available integrated circuits for this purpose, such as TTL integrated circuit 74150 :
that contains a Data Selector 1-of-16 , or TTL integrated circuit 74157 contains four data selectors 1-of- 2 , or integrated circuit TTL 74153 that contains two data selectors 1-for-4 , or integrated circuit TTL 74151 that contains a Data Selector 1-of- 8 , these last three with the following list of terminal "pins"
Functionally, the Selector Data 1-for-2 as the four that contains the integrated circuit 74157, can be regarded as constituted in the following way inside (the logic circuit on the left and right logic circuit are equivalent, the only difference is that the right logic circuit is constituted with NAND blocks that are easier to implement directly in microelectronics that blocks OR and AND):
As indicated in the Table of Truth, when the terminal selector (S) elect is wearing a " 0 " then it will pass the value you have in the terminal D0 , either " 0 " or " 1 ", while when the terminal selector is wearing a " 1 ", then it will pass the value you have in the terminal D2. In the case of integrated circuit 74157 , it only takes a selector terminal, which in this case is the terminal SELECT A B (in the "pin" integrated circuit 1), which is used to select a signal bit A (eg 1A, the terminal 2 of integrated circuit) or signal B (1B, the integrated circuit terminal 3) channeling out through the terminal And for integrated circuit (1Y, the "pin" 4). The action of the terminal selector affects all four bits of words and A B alike. Thus, this circuit is capable of choosing among the four bits of the word A or four bits of the word by sending B simultaneously (in parallel) out.
With respect to the integrated circuit 74153, one of four possible binary values \u200b\u200bthat may have the word selector s1s0 channeled to the output ZA (terminal 7) one of the four bits of the entry into I0A , I1a , I2A I3A or , and while the exit channel ZB (terminal 9) of the four bits of the entry into I0B , I1b , I2b or i3B .
And in the case of the integrated circuit 74151 , only supports a single eight-bit binary word at the entrance, and at any given time only one of the bits is channeled out (by the output terminal Z ) depending on the binary values \u200b\u200bthat has the word selector S2 s1s0.
can interact with different combinations of the latest integrated circuit through visual interactive program maintained by the University of Hamburg in Germany, through the following link (requires that the computer is enabled with the Java accessory program):
http://tams-www.informatik.uni-hamburg.de / applets / hades / _______
Webdados / 10-gates/40-mux-demux/SN74151.html
PROBLEM: To build a three-input logic circuit A , B and C , which has the following truth table:
instead of building from the three basic logic functions is desired an integrated circuit switch data obtained at low cost in the market, in which the sorting lines S 0 , S 1 and S 2 be used as inputs A , B and C and data lines will be activated in a fixed with "a" and "zeros". Solving this problem using:
1) A Data Selector 1-for-8
2) A Data Selector 1-for-4
1) Using a data selector 1-of- 8, the solution is straightforward:
As you can see, to take the ABC entry condition " 000, the first value in the" 1 "passes to the exit. ABC to take the condition " 001, the second value" 1 "in the list passed to the output. And so on. Note that successive values \u200b\u200bwill be output following a binary count ascending sorting entries were taken directly from the Table of Truth.
2) To carry out a simplification which we can use a Data Selector easier than sorting has only two entries, first grouped pairs successive equal B and C and compare the output of each pair with the values \u200b\u200bthat should be taken to the input according to the Table of Truth:
Here the output will always be " 1 " regardless of the value take input A.
In this case we can see that the output is the complement (the logical inverse) of the input A.
In this case, the output will always be " 0 " regardless of the value that drink A.
Here the output will take the same value take input A.
Given the above, using a Data Selector 1-for-4 the design will look like this:
or more specifically, in the final design:
Note how easy and economical it is to design logic circuits using a Data Selector. The procedure used in this problem can be extended to more variables without difficulty. Although a Data Selector 1-of-16 as TTL integrated circuit 74150 is more expensive than a Data Selector 1-for-4 as the integrated circuit TTL 74151, the difference in cost may not be much to justify going to more economical design as we did in this case, simplifying the design so as to require a Data Selector 1-for-4 in place of a Data Selector 1-for-8, taking into account that the rationale behind simplified design will be harder to read for technicians who will maintain a team utilza simplified design. On the other hand, if you are going to produce tens of thousands of computers that will be offered for sale on the market, then a price difference of a few cents from an integrated circuit and another can result in significant savings of several thousand dollars .
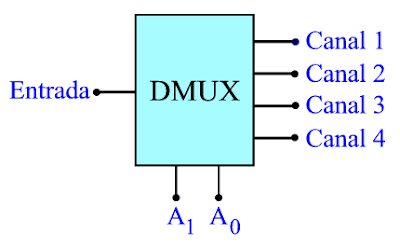
PROBLEM : The next unit, commonly known as demultiplex unit (DMUX) sends the information made its entry to only one of the four output channels.
The desired channel is selected using the binary word A 1 A 0 as selector. What is the internal configuration? Extending the design for a demultiplex unit that may be able to send your entry to one of eight output channels.
The internal configuration is as shown below:
The action of "switching" required DMUX block is essentially as follows:
One way of representing the internal configuration of the DMUX unit where there is still a domestic presence a "decoder" of S 1 S 0 albeit in a not so obvious is:
In this representation, is still carrying out a decoding binary word S 1 S 0 making it one of four independent lines for each of the four combinations of "ones" and "zeros" start S 1 S 0 , in order to allow passage by only one of the four blocks in DNA time. However, since within a "black box", this is entirely equivalent circuit shown above. The latter design can be extended to handle eight channels of output with the addition of an additional selector terminal S 2 with which the word selector will S 2 S 1 S 0 , and adding four blocks AND also three additional tickets each (enlarge image):
One way to symbolically represent a demultiplex DMUX block in the schematic diagrams involves the idea of \u200b\u200bwhat you're doing (an opposite function to the function by the MUX block) is as follows:
PROBLEM: describe the joint operation of a multiplex unit to a demultiplex unit.
In real life, invariably when a system uses a multiplexing unit MUX is because it will always paired with a demultiplexer unit DMUX, and so both should work together through the selector acting simultaneously and in a synchronized on both MUX and DMUX units as follows:
The obvious reason to have to resort to a combined MUX-DMUX is because it is often necessary to send (or receive) information from different devices when only one communication channel available to digital transmission. An example of this would be several computers connected from one location to the Internet, sharing a single telephone line. As digital information from various computers can not be sent simultaneously over a single channel of communication, the time of the channel is "shared" equally, giving a brief time at the computer # 1, after which it is given a short time at the computer # 2, and so on, after which it will begin a new round giving it a short time to the computer # 1, followed by computer # 2, and so on.
From the point of view of the multiplex unit MUX, the information will go out in a manner as shown below:
Schematically, in this circuit the first out, first to be put the only line available for external transmission of data, is the first data "A" represented by a red triangle in the upper left, the first information on the first channel of communication. After that, it is sent through the second data line "B" represented by the first green parallelogram taken from the second communication channel, the first data on the second channel of communication. This is followed by the data "C" taken from the third channel of communication identified by a blue circle. Finally, it sends a data "D" taken from the fourth channel of communication, represented by a magenta diamond, after which the cycle begins again. Note how leave "apparently" scrambled data through the only available line for external data transmission. To get some sense of the data being sent, the receiver must necessarily be synchronized with the sending of data. That is why the selectors of MUX and DMUX must be connected in some way to go ruteando ( routing) information through appropriate channels without any possibility of revolt ends.
synchronized action selector MUX-DMUX shown outlined in the following GIF file ( zoom in to see the animated action):
PROBLEM: the truth table of an electronic circuit shows the following voltage values \u200b\u200bfor both A and B inputs to the output. What role does the positive logic circuit? What role in negative logic?
Using positive logic, smaller attach to the voltage (or close to zero volts, or more negative) the value of "0 " and the higher voltage (3.2 volts in this case ) the value of "1 "
This is a NOR function.
Using negative logic, we assign the higher voltage value " 0 " and voltage smaller the value of "1 ," that is the opposite of what we did before:
This is a NAND function.
PROBLEM: The circuit shown below is called a "gate" in a different sense that is often given to the logical blocks AND, OR and NOT. What action is carried out in accordance with the value taken by the terminal T ?
Given the action of the functions AND, when the terminal T the value "0 , the output of the gate is" 000000. When the terminal T the value "1 , the output of the gate is A 6 A 7 A 5 A 4 A 3 A 2 A 1. That is, the terminal T is acting as a trigger that stops or allows the passage of information based on the value purchased. Suppose that
A 6 A 7 A 5 A 4 A 3 A 2 A 1 = 100110
would then have the following cases:
PROBLEM: Analyze the following circuit constructing a truth table for it.
In the analysis of these circuits, it is desirable to find those combinations of inputs will always produce an outcome consistent regardless of the values \u200b\u200bthat make the other entries. To go "filling" our Truth Table initially blank, we can fill the whole column for the output values \u200b\u200bI realizing that this output is connected directly to input D, so that when the input D is " 0 " exit E is also " 0 " and when the input is D " 1 " E output will also be " 1 ." Similarly, we can see that the action of DNA of three entries, which gives the output F only produce a " 1 " the output F when we ABC = 100 both D = 0 to D = 1 , allowing us to fill the column to the output F immediately with "some" and the rest zeroes. Also, when the input A has the value "1 ", thus opening the gate that represents the DNA that provides the output E , just any entries B or C have the value of "1 " to output E also has an " 1 " and only when both inputs have a value of "0 " output will be "0 ." Put another way, all the combinations for which A = 1 and B = 1 "light" E output, and all combinations for which A = 1 and C = 1 also "light" E output. When both inputs and B C are " 0 " E output will always be "0 ." With respect to the output G, this requires that the input is B " 1 " and also A is " 0 " or C is " 1 " for output G is "light" with a "1 ." And with respect to the output H , this will be " 1 " only when the inputs and A C have the courage AC = 01 (by the action of feeding the first AND OR I output) or A entries, and B C have the courage ABC = 110 (by the action of the second AND OR feeding the output I), where " 0 "in all other cases. So we can go fill a truth table without having to go look at individual combination possible "ones" and "zeros" at the entrance, which eventually can be completed following Truth Table:
comparing ABCD entry to the circuit (taking tickets together as one word binary) output EFGHI , see something very interesting: the output of the circuit is identical to the input from ABCD = 0000 to ABCD = 1001 (which is a binary count up), after which from ABCD = 1010 forward the output begins to "count" ascending again in binary form starting again from zero. Put another way, the output is giving us the binary number placed at the entrance converted to equivalent BCD system. If we connected the word FGHI a decimal numeric dial (using a decoder as described in a previous problem), we would be reading in our decimal equivalent of binary number placed at the entrance. E output when "on" with a " 1 " is used to indicate that we are in a recount decimal, and could also be used to "turn on" a second light for tens of our system decimal.Este circuit is an example of what is known as a translator , in this case a BCD binary translator .
PROBLEM: Below is the schematic of a probe logic of economic construction can be used to confirm the presence of a " 0" or a " 1 "at any point of a logic circuit. Explain the operation of it.
Although the diagram indicates that the logic probe to be supplied by a voltage source of +12 volts, not really require a separate external power source, as usual practice is to feed these probes are taking the same power circuit being analyzed.
The input to the probe tip is in the so-called probe, which can put a " 0 " or " 1 " as the logical condition of the item being measured . This information will be made to the input of a NOR on the terminal # 1 integrated circuit (IC1a) 4001 that is being used for input. Since the other terminal # 2 of the integrated circuit is placed in the level of zero volts, which is a " 0 " logic, the only thing that will change NOR output is the value placed on your terminal # 1. If the tip "probe" is a " 0 " then the output of NOR in the terminal # 3 is " 1 " and if in the end "probe" is a " 1" output of NOR will be "0 ."
The output terminal of the NOR # 3 feeds an input terminal of another block NOR (IC1b), which since its other input is connected to 0 volts is being used simply as a signal logic inverter NOR sent by the preceding one.
Following the path of binary values, if the value to "probe" is " 0 " NOR output right will also be a " 0 ", which equals to the midpoint between the electrical resistance to zero volts. This causes the electrical current flows from the power source through the green light emitting diode LED1 (LO ) continuing to the input terminal # 4 of the NOR (the " 0 " to the output of NOR possible electric current can flow inward NOR, as the electric current always flows from the positive or " 1 " to negative or " 0 ") instead of flowing through light emitting diode red LED2 remains off. The electric current is limited by the presence of superior resistance of 680 ohms is worth just what it takes to design the LED can be illuminated properly. In essence, a " 0 " at the entrance to "probe" LED lights green to indicate a logical condition of " 0 " or LO (low).
The situation changes when the "probe" is wearing a " 1 " which means that in the terminal # 4 of NOR right has a " 1 " that can be taken as essentially equal to the voltage of + 12 volts. Since both ends of green light emitting diode LED1 is now at the same electrical potential of +12 volts, no current can flow through a green LED, which will shutdown. Instead, this " 1 " will be putting a voltage of +12 volts to the red light emitting diode LED2, which when connected across the potential of zero volts will have a voltage difference of 12 volts applied between two terminals, which will cause LED2 drive with power limited by the resistance of 680 ohms just what is required for the LED can be illuminated properly. In essence, a " 1 " at the entrance to "probe", the red LED indicating a logic condition "1 " or HI (high) point being measured.






















































0 comments:
Post a Comment