Does Anyone Have Razor Buggy In Store

2: The three basic logic functions

icon as is suggested above since the beginning of all chapters of this book, there are three building blocks with which we can build all the logic functions capable of being conceived by the human mind. These are the building blocks on which rest all the computers used today, from home computers to the most powerful supercomputers.

begin our introduction to the world of digital logic reviewing the principles of operation of electromechanical relays , which rely on the well-known phenomenon that when you apply an electrical current to an insulated wire that is coiled around a metal cylinder (or even wrapped around a nail regular) creates a magnetic field that can attract other metallic objects, as shown by the following figures:

In the left figure, by applying to the wire wrapped around a metal cylinder voltage provided perhaps by a battery, the voltage produces an electric current which in turn creates a magnetic field, whose "lines of force" magnetic can act on metal objects near them. And in the right figure, by removing the voltage, the magnetic field disappears. On top of both figures have drawn a movable metal slat acting as an electric switch or switch , which is attached to a spring (not drawn) that pulls up. As can be seen, by applying a voltage to the wire coils, the switch Electric closes, being enabled to allow the passage of electric current, while failing to voltage by the action of the spring that pulls up the contact slat breaks. To simplify our analysis, we apply voltage to the wire, which may be 1.5 volts, 9 volts, or some other value, we will call simply " 1 (one). And the absence of this voltage will call simply " 0" (zero). Thus, by applying a " 1 " the relay, electrical contact placed on top of it is closed, and by removing the " 1 " (which is the same as applying a " 0 "), the Electrical contact is opened. Since the electrical conduction terminal coiled wire (which we will call coil) is electrically independent (isolated) of electrically conductive terminals that are connected by the action of the slat set over the coil, the value to take input voltage to the coil of the relay, either " 0 " or " 1 " will not be affected by what happens to the output thereof llamándosele here "out" at any voltage signal that can be transmitted through the upper slat to be closed by the action of the magnetic field of relay activated by a " 1 ."

Here, courtesy of HowStuffWorks.com site, we have an animated file that shows how an electromechanical relay to close the switch that allows the relay coil is energized by a battery, thereby allowing the closure of the circuit to another battery can light a bulb ( zoom to see the animation in action):

Although the battery (power supply) which energizes the relay coil is one and the battery that turns the focus is different, the figure suggests that it is providing equal batteries the same voltage level (eg 5 volts) to both the relay coil as the focus, which suggests that instead of having to use two batteries could use a single battery, the same battery for both acting jointly purposes. This is important because " 1 " that activates the relay would be in all respects the same " 1 " that turns the focus. Consider then the following circuit consists of two relays, in which the springs that normally pull the levers (or slats) connecting the relays are shown in red:

normally any source of direct current as the batteries in the car has a positive (+) and minus (-), but for purposes of simplification and schematic diagrams are usually refer to negative (-) and electrical ground (in English, or ground GND). This allows us to "forget" the negative and simply talk about implementing a " 1" (voltage) or a " 0 " (no voltage) to a terminal as the terminal A or as B terminal. In this diagram, if we apply a positive voltage (here also called simply " 1 ") In the terminal A , the relay is energized. Note that in a relay contact upper left connector have a voltage of +6 volts, which when activated terminal A with a voltage of" 1 "and close the upper port of the relay can pass to the other terminal of the same. However, this voltage will not reach the far left of the configuration, designated as Q , if the input of the relay on the right side has not been activated also its terminal B with a " 0 " because it connected the terminal contacts of both relays series, one after the other. The only way in which the voltage of +6 volts can be reached from the left side of the configuration to the right side at the terminal Q is if both relays are energized with a " 1 " in the terminal and A B . Suppose for a moment that we have developed here the relays so that the voltage required to energize any of them will be of +6 volts. This allows us to call the +6 volts simply as " 1 ." And we can make an interesting statement: if the entries at terminals A and B are " 1 " then the output also Q is "1 ." But if any of the inputs at terminals and A B or both is " 0 " then the output is "0 ." Only when both inputs are "1 " will output "1 ." Only when A and B are both " 1 " the output is also " 1 ."

We can represent the operation of this type of circuit in a more concrete and easier to read:

The English translation of the English word " and " is the word and . This is precisely the word we use to identify any combined system shows a behavior like we just saw. It is common to represent a circuit of this nature as follows:

This block is best known as AND function as already said your English to English translation of the word " and "as in the phrase" homeland and freedom, "and is itself a basic logic function . This will be one of our fundamental building blocks. We can represent their properties in a table known as Truth Table shown below:

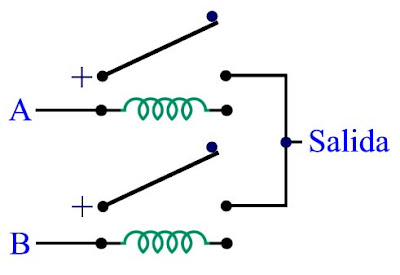
Now consider the following circuit built with electromechanical relays:

If any voltage is not applied in the two input terminals and A B , the coils of both relays are not energized and the switches of both relays will remain in the positions shown in the diagram. In this case, the voltage (+) we will call " 1 " will not reach the output , thus having no any voltage on it. The absence of voltage at the output identify it with a "zero" or " 0 ." The situation changes when we apply a voltage (or " 1) in the terminal A , in which case the coil is energized and" pulls "touch down, connecting the voltage (+) to Exit , whereupon the output status will " 0 " the condition "1 ." This " 1 " remain in the output while a "1 " applied to the terminal "1 ." On the other hand, when we apply a voltage (or a " 1) in the terminal B, in which case the coil is also energized and" pull "touch down, connecting the voltage (+) to Exit , whereupon the output status will " 0 " the condition "1 ." And if both input terminals and A B are energized with a " 1", the output continue to receive the voltage (+) or " 1 " by the two pathways. Basically, we have a circuit in which the output will be " 1" when either input or A B have a " 1 " applied to it.

The English translation of the English word or "is the word or . This is precisely the word we use to identify any combined system shows a behavior like we just saw. It is common to represent a circuit of this nature as follows:

This block is best known as OR function as already said your English to English translation of the word " or "as in the phrase" homeland or death, "and is itself other basic logic function . This is another of our fundamental building blocks. We can also represent their properties in a truth table as shown below:

Here's the meaning of the word OR . The output of the circuit will 1 if the input A or B entry has a value of 1 .

Finally, we now consider the following circuit built with one simple electromechanical relay, which when no voltage is applied to one input terminal A (which equals to zero volts or " 0 " on input terminal), the positive voltage (+) to designate as " 1 " logic goes directly to the output :

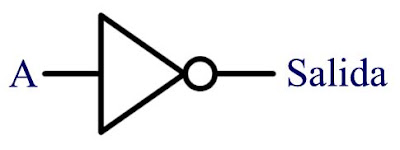
Suppose now that a voltage is applied (a " 1) to the input terminal A . To energize the coil of the relay, becoming a magnet for the action of electric current "pulling" so the switch above it down, the upper contact connecting the output to a positive voltage source (a " 1) drops from its normal position, disconnect the positive terminal voltage, which is equivalent to waive any of output voltage , which can be taken as "zero" (" 0 ") software. Apart from the unnecessary details, we have a component in which when the input is " 0 " output is "1 " and when the input is "1 " falls out " 0 ." This is what we commonly call as a logical investment . This component is therefore an investor .

common symbolic representation is a component that works in this way in the following form:

is important to clarify that what he really represents the investment function is the "bubble" placed to the right of the triangle. The triangle itself, historically, sought to point out that in addition to investing was conducting an amplification eletric signal prior to correct any damage that would have been, and indeed the symbol without the bubble is known as buffer , although the buffer itself does not do any processing of information because a " 0 " since its entry passes as a " 0 " to its output and " 1 " since its entry also goes unchanged as a " 1 " to its output. It is common in many logic circuits using only the bubble either one or multiple entries and / or one or more of the outputs to indicate that at this point is taking out an investment. It is important to note that, in general, the bubble only has this meaning only when it is "attached" to a basic logic functions of any component or derivative thereof.

symbolic block shown above is best known as the function NOT (the word comes from the English word Not in English means " not, as in the phrase of denial " carlos not an architect) and is our third basic logic function. We summarize its properties in the following truth table:

These are the only blocks that need to build any computer capable of running a program like Windows or Linux. Many of them are needed to assemble a computer, of course, but the tight integration of millions of transistors on a small high-density integrated circuits can achieve the construction of super-computers that only two decades ago still would have seemed impossible to achieve. Manufacturing technologies have been diverse, from primitive electromechanical relays which IBM built the Harvard Mark I computer in 1944 in the United States at the initiative of Dr. Howard Aiken, and which computer Konrad Zuse built the Z3 in 1941 in Germany , through the electronic vacuum bulbs (previously used for the construction of radios and televisions "primitive") with which they built the ENIAC computer, up to transistors and integrated circuits which enabled the construction of microcomputers and minicomputers, culminating with the first chips that began to be manufactured Motorola and Intel that allowed the manufacture of home computers such as the one the reader is in these moments in their hands. However, behind all technological alternatives, one thing has not changed, and this is the fundamental theory that makes them operate, based always on balance in only three basic logic functions, OR block, block and block AND NOT .

OR logic functions AND and can have not just two but three or more entries each. Consider, for example, a AND of three entries:

Since the two-input AND output is 1 only when all tickets are 1, extending the definition we have that in three-input AND output will also be 1 only when all inputs are 1 . With this in mind, we can immediately construct a truth table for AND three entries:

Similarly, we can make a similar extension of the concept of the OR block for an OR that has more than two entries, where extending We define the output of OR in any number of entries will 1 when either input or a combination of any of the entries has a value of 1 .

now consider what happens when you connect a a OR NOT as follows:

applying all possible combinations of ones and zeros in the entries, we get the output taking every possible combination takes into account the properties of the OR and NOT action's investment, which we can build the following Truth Table:

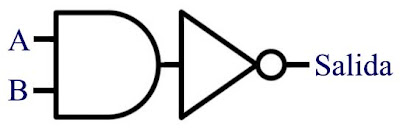
We have a circuit that produces a 1 to the output only when both inputs are 0. This configuration is best known as the function NOR (NOR word is a contraction of the words NOT - OR , which are the elements used to build this configuration) and is represented as follows:

then study what happens when you connect a a AND NOT as follows:

Table Truth for this circuit shall be as follows:

We have a circuit that produces a 0 to the output only when both inputs are 1 . This configuration is best known as NAND function (NAND word is a contraction of the words NOT - AND , which are the elements used to build this configuration) and is represented as follows:

functions NOR and NAND are clear examples that show how you can use the three basic logic functions to construct more complex functions.

now consider the following situation:

The question we ask is: What will the output of OR to enter words and 01100 11001 in your posts ?

To answer this question, we note that the first bits to enter the OR are the last bit of the word 01100 (ie, a 0 ) and the last bit of the word 11001 (ie, a 1 ). The output from the OR is therefore a 1. Then, the following bits are entering the penultimate word bit 01100 (ie, a 0 ) and the penultimate word bit 11001 (ie, a 0 ). The following output from the OR will therefore 0 , making their departure and has formed the word 01 . Thus, we see that its output will be the next word:

11101

Since the word in the output of the OR is different from words to their inputs, say that has been carried out data processing. This is the fundamental purpose of all logic circuits.

Now suppose we are presented with an electronic component in which the natural voltage levels to the system are +5 volts and 0 volts. This electronic component has two input terminals A and B and an output terminal. By applying the following levels at their inputs produces the following voltage levels at its output:

Designating the higher voltage (or positive) to +5 volts as 1 "and the lower voltage ( or more negative) as " 0 " Table of Truth takes the following aspects:

The circuit behaves as a function OR .

In this last example, we might well have taken another equally valid convention. We could have identified the voltage of +5 volts with a " 0 " and the voltage of zero volts with a " 1 " which makes us different from other Truth Table. This is what is known as negative logic . In order to avoid confusion, we have failed and we continue to refrain from using this approach, but once you have mastered the principles of positive logic and negative logic are as valid one as the other. Let us at least with this example so; build the truth table assigning the level of +5 volts logic value "0 " and the voltage of zero volts a logical value of "1 ." Then the truth table is obtained as follows:

circuit behaves like an AND function. We

then the logical behavior of a circuit depend on the assignments we give to their voltage levels. The practice of appointing the higher voltage (or positive) as 1 "and the lower voltage (or negative) as" 0 "is known as positive logic. The practice of appointing to the lower voltage (or negative) as 1 "and the higher voltage (or positive) as" 0 "is known as negative logic .

The remainder of this work, unless otherwise indicated, shall be used only positive logic.

With the three basic logic functions can build more elaborate circuits of increasing complexity, the analysis can be carried out assuming all possible combinations of "ones" and "zeros" at the entrance, and following the flow of each combination of values \u200b\u200bto see what we have to check out the role of the circuit. By convention, the logical circuit diagrams are drawn so that the signal flow is traced to izquieda to right. Following is a diagram of a simple logic circuit whose two input terminals and to b be found two "ones" (" 1):

In AND we have in the far left of the diagram, we have two one (1 ") at the entrance, which produce a" 1 "to exit. This " 1 " at the exit of DNA is inverted by the NOT, becoming a "0 ." Thus, we have the inputs of the OR at the far right of the diagram a " 0 " and "1 , which produce a" 1 "to exit. We need to test other combinations of other values, which are to = 0 and b = 0 , to = 1 and b = 0 , to = 0 and b = 1 . This method of tracking signal values \u200b\u200bcan be applied to any logic circuit, no matter how complex.

As we build more and more logic circuits complex, the wires are connected to each other is shown explicitly connected with a dot connector, while the wires just above the cross one another without connecting not have the connector point:

However, in the joints "T" in the schematics:

is always sobreentenderá that there is a connection between the two wires, either with or without the presence of "point "connector (it must be some caution, since in the simulation of logic circuits in a variety computer programs is essential to always add in the simulation diagrams "point" connector, as many of these programs are not prepared to recognize this convention)

In designing logic circuits, one of the things that is not allowed is connect directly to a single point out of two logic functions in a way which is shown below:

Since it has been defined " 1" as the positive pole the power supply (eg +5 volts) and the " 0 " as the negative pole the same power source (known popularly as "electric earth"), the situation shown equivalent shown nothing less than a short circuit . And while the vast majority of discrete integrated circuits that are sold today have built-in micro-structure of resistors and transistors which prevent a short circuit of this nature could damage, limiting the current flow through same, the output of a logic circuit of this nature is at best undefined.

If for some reason insist on wanting to connect together the outputs of two (or more) basic logic functions, we can do using diode rectifiers, which conduct electrical current in one direction but not in the opposite direction. Physically, in a real circuit, these components have an appearance like the one shown below, where the band placed at one end of the component indicates the polarity of the cathode (the component that is connected to the negative pole power source when you want this power drive component), corresponding to band played by the arrow in the symbol representing the diode on the right:

rectifier diodes
Using the above logic circuit and "corrected" present the following Appearance:

In this circuit the higher DNA is putting a " 0 " on its output terminal while the bottom is NOT making a " 0 " on their own. The voltage associated with " 1 " logical normally produces an electric current flowing into the " 0 " logical. But in the rectifier diodes, the electric current can flow in the direction of the arrow, so that if the tail of the arrow is a " 0 " and the tip of the arrow is a " 1 "as with the superior DNA, the diode will not allow the current flow and act as if the wire was cut, effectively disconnecting the DNA of the combined output. In other words, the " 1 " inverter NOT is the winner. But if the output of NOT be " 0 " and the output of AND was " 1", then the DNA would win. And if the output of both was " 1, then both put a" 1 "logic in the starting line and there is no logical contradiction (or short). But if we look at these functions, we realize that the inclusion of diodes in the circuit means that the two provide the equivalent of the OR, with the disadvantage that the diodes provides no signal amplification. Good design practices suggest we remove the two diodes and replace them with an OR block.

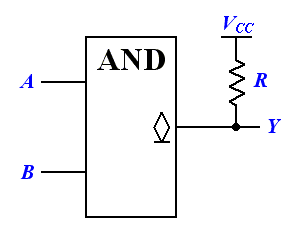
A major exception to the prohibition of connecting directly to the same extent the outputs of two or more logical blocks, and this happens when you are using integrated circuits able to implement something known as the wired logic (wired logic), also known as open collector logic ( logic open collector), which has to do with the fact that such circuits built from bipolar transistor (a bipolar transistor Basic has three terminals, the base , the issuer and collector ), use the terminal called "collector" of bipolar transistor "open" mode (no connection required) to carry out this function, being by designed to connect to this same point to which we must also add a resistor connected to the positive voltage power supply, as shown in the following diagram in which are connected the outputs of two blocks NOT:

rule, to use the wired logic or "open collector logic" in the junction is carried out AND function, this is the reason why in the above drawing was outlined AND around the junction of the outputs of the NOTs. If we put a " 0 " at the entrance of the two NOTs, the output of the two will " 1 " and by the action of DNA at the junction point of the output circuit And be worth " 1. If either input or A B the NOTs is " 1 " which will be invested to " 0 ", then the action AND on the output of both the common output and have a value of "0 ." And if both inputs are " 1 ", then the output will And " 0 . We then have a circuit in which the output is "1" only when both inputs are 0 ", which is in effect the action of a NOR circuit. The symbol A · B placed on the picture to represent the logical value output And this action is DNA in the symbolism of Boolean algebra, the discussion will be postponed and clarified in the next chapter .

Not every family of integrated logic circuits can be connected in this way. Note that within blocks was drawn symbol NOTs a small diamond with a horizontal bar placed below it. This is the symbol used to indicate in the schematic diagrams are using wired logic components working under, which is specified by the technical convention IEEE/ANSI-1984 indicating that any component whose output can be wired to another component under wired logic must stand drawn into the logic block near the exit of the diamond symbol with horizontal bar placed under Diamond:

As an example of this symbolism, then we have two open collector DNAs of three entries each one, with their outputs connected directly giving the equivalent of a six-input AND total:

For example we saw where we connect directly to the outputs of two inverters logical NOT, possibly logically we would use as NOTs open collector which provides an integrated circuit as 7405, which includes six investors and whose relationship NOT terminal "pins" is shown below:

The following show the outputs of three NOTs of this integrated circuit connected to the same point under the scheme of "collector open "

Some other integrated circuits whose operation is based on" open collector logic "are the 7403 (which provides NAND gates using the same ratio of terminal" pins "that integrated circuit 7400 is not "open collector"), the 7409 (AND gates which provides the same ratio of terminal "pins" that 7408) and 7433 (consisting of NOR blocks and has the same ratio of terminal "pins" that 7402).

To carry out experiments with basic logic circuits designed or whose behavior we want to verify, we have two alternatives. The first is to build a prototype experimental using integrated circuits that can be procured on the market. In the market have appeared (and continue to appear) many "kits" low cost to facilitate the work of the experimenters. Below is one of the first to appear in the seventies thanks to cheaper electronic integrated circuits, Digital Logic Microlab, which was sold by Southwest Technical Products and which was popular for some time by the magazine Popular Electronics:

The simulator implements the logic shown above electronics and obsolete technology engineers call RTL (Resistor Transistor Logic), which ended up being displaced by another much faster technology, called TTL (Transistor Transistor Logic). RTL technology used by this simulator does not directly implement any of the basic logic functions studied here, as its fundamental building block is the block NOR. If we look closely at the middle of the simulator, four NOR blocks, which are obtained from an integrated circuit, the basic integrated circuit RTL family, the 4001. Note that the NOR is represented in the simulator with a triangular symbol and "logical negation bubble" placed on the tip of the triangular symbol, according to what was customary in those days. If we had one of these simulators on hand and what we saw inside, we find that the four blocks NOR interface accessible through the posts on the dial from an integrated circuit that looks like this:

An inspection to the schematic of the integrated circuit shows in their relationship that actually has four terminal blocks inside NOR:

Then we have another "laboratory" whose purpose is to go home by introducing new generations of technicians and engineers to the world of digital logic, in which we can see some of the logic functions covered in this chapter as well as other logical functions more elaborate study of which will be left for later chapters:

Thanks to the power of desktop computers, there is an alternative much cheaper and much faster to "build" a prototype using several combinations of logic circuits, and this is to use a simulator software, or a program running on the computer for taking the conventional logic symbols irlos catalog for "connecting" on the computer monitor. What is done here is to carry out a simulation of a virtual experiment where there is a single wire in sight, everything is done schematically from the keyboard. One such simulator is the simulator software Digital Works, which costs about eighty dollars:

There are also free high-powered simulators that can be downloaded free from the Internet. One is the logical simulator Logisim , developed in 2002 by Carl Burch, which can run on any home computer that has implemented the Java platform (now the majority does, and those who do not have can also be obtained free from the Internet):

Logisim
The simulator software can be downloaded free from the following link:

http://ozark.hendrix.edu/ ~ burch / logisim / index_en.html

Another free program is Digital Simulator , developed in 1996 by Iwan van Rien, which is not an executable program in the strict sense of the word, but it is a applet Java platform, which has to be installed on the computer before the Digital Simulator can run. The source folder containing all you need to run the simulator can be downloaded for free as a zip file usually called DigSim.zip , which when unzipped into a folder does not show any executable file from which you can "shoot" the Digital Simulator, and the only thing displayed is the famous "classes" in which it does Java. Anyway, assuming the computer has already installed the Java platform, you can quickly press the mouse of the computer on any of the files ending with ". Html. This will invoking the browser you have installed the computer (eg Internet Explorer), and when invoked the Java platform browser will be invoked by the content of the file. "html" is selected, after which should see a window like the following (in this case, we have chosen the window that appears when you click a file entitled "sim_and.html" which shows the action of the AND function with two switches connected in series, and block the action of logical AND):

Once the window appears, go easy matter choosing from the menu line components that we want to be adding a new track you want "Build" after deleting everything from selecting the menu option " File -> New ." At the option labeled "Passive " can select wire connectors (Wire), a connection of two wires intersect (Junction) to connect them electrically, the positive power supply Vcc (equivalent to our " 1 "software) that appears in the upper left corner of the window work, the negative or" ground "power (equivalent to our" 0 "software) which will also appear in the upper left, a switch (Switch) and a push button switch (Push button) which can be "dragged" into the interior of the window by holding down the mouse on the computer. At the option labeled "Ports " we can select one of several logic gates also will appear in the upper left corner of the window, either a NOT (inverter), an AND, an OR, or any other blocks. In "bi-stable" sequential can select components that will be addressed later in this book. Under "Display " can be selected LED light-emitting diodes to obtain visual confirmation "light" on the presence of a " 0 " or a "1 "And the" Special "we can choose other more sophisticated components such as a generator of" pulses "(Oscilator) and even a" logic probe "to measure at some point in a circuit and see if we have a " 0 " or a "1 . The action of the simulator can be launched by pressing the button with a yellow lightning drawn into it. And if you have to build a logic circuit by the user self sure how this window works "Java applet, you can select one of several examples included in the package with the line option from the menu" File -> Open example. One thing you can do the program is stored in computer files designed circuits, due to security measures implemented by Java.

The Digital Simulator developed by Iwan van Riener was subsequently updated with some improvements made by Deborah E. Lynch and Phil White, and renamed in Digital WorkShop . In one of its most common file- DigiSim.zip which is made in the Digital Workshop " to be unpacked produce multiple folders and an executable file, Java file Digisim.jar . To jump-start the Digital Workshop, just click the mouse icon representing the Digisim.jar file, which the user can start to "assemble" immediately all logic circuits. One thing I find the user is that the Digital Workshop, unlike the Digital Simulator, enable your browser does not require the computer to operate, can walk by itself (this is precisely one of the advantages of executable files with extension " . jar "). Since the mode of the Digital Workshop is almost identical to the mode of the Digital Simulator is just described, it is not necessary to repeat the details here.

Yet another program that can be downloaded for free, which by the way was rather expensive but now its creators made publicly available to the world for free over the Internet, is the program MultiMedia Logic, whose visual interface looks as follows:

This program can be downloaded free of charge from several sites as follows:

http://www.softronix.com/logic.html

Another extremely good option for "build" logic circuits (simulated) on the monitor of a computer is the student version of PSpice program , which can be downloaded without charge from the following address:

http://www.electronics-lab.com/downloads/schematic/013/

This program still in its student version is a program so complete and sophisticated than the download file has a size of 28 megabytes, so download the same is not recommended over a low speed Internet connection.

addition to the above programs that allow us to design and "build" logic circuits (simulated), immediate alternative exists to see the action of logic circuits "in vivo" interactively, as if they had at hand a board with actual physical components. As an example, we recommend visiting the following website which the user can "play" through "Mouse" of the computer with various logic gates, "turning on" with "some" or "off" with "zero" input terminals, immediately seeing the effects on output (or outputs) of the logic circuits in the diodes emitting diodes (LED) Simulated
http://www.dst-corp.com/James/LogicPrimer/Gates.html


interactive logic circuits shown in this last link was created precisely to the program and MultiMedia Logic mentioned.

Another comprehensive site, maintained by the University of Hamburg in Germany, provides programs to show visitors a visual interactive behavior of logic circuits just to see. In the following address:

http://tams-www.informatik.uni-hamburg.de/applets/hades
______ / webdemos/10-gates/00-gates/basic.html

we can "change" inputs of logic gates and immediately see how it changes the output of the same.

Yet another interesting place to visit, in which the user can have a good "playing" a good time with simulated logic gates such as displaying the link above, is this site maintained by Professor Constantinos E. Efstathiou, Director of the Laboratory of Analytical Chemistry, National University of Athens Kapodristiana:

http://www.dst-corp.com/James/LogicPrimer/Gates.html This page

Professor Efstathiou, logic simulators appear on the right side of the screen where the options to simulate the elementary gates we have seen are obtained from the menu "Circuits" under the options, "Gates 1 and Gates 2 "(there are other options, which will be addressed in due course in other chapters of this book when the reader is sufficiently familiar with the behavior of the three basic logic functions).

provided links were still valid at the time of this work published online in early 2008. Unfortunately, there is one link in Internet whose life is assured over term. Anyway, in case they disappear some of the links mentioned above, there is always the possibility that previously recommended programs can be found elsewhere or even that they can find better programs we have been discussing. It's all about using good equipment such as Google search.

Although logic plays no role whatsoever, a component which appears with some frequency in the world of digital logic and light to provide some kind of visual information to the user is LED (light emitting diode or LED ):

which is not only a diode in the technical sense given the word (a component in which electrical current can flow in only one direction but not in the opposite direction) but is also capable of emitting light a certain color when a voltage is applied with the correct polarity (with reverse polarity voltage, the LED will not conduct any current or issue any light.) The LED is generally built with a shorter terminal (cathode called terminal or - ) than the other (called the anode + or terminal). Below is a LED together with the symbol which is represented in the schematics:

light emitting diode LED is available in several colors, either red, green, blue, or amber as we have below

The simplest scheme to "ignite" a light emitting diode LED with an ordinary battery E is as follows, in which simply apply the battery voltage setting attention to proper polarity:

resistance R shown in the schematic main objective is to limit the extent of preventing electrical current has a short circuit damage to the component and system, but also aims to set the current value with which the LED may issue its brightest possible without damage. Not to be the LED diode ideal but a real diode (LED ideal is one that being polarized in a sense acts as an open circuit and to be polarized in the opposite direction acts as a closed circuit without loss voltage across it), when an LED is driving there is a small constant voltage drop V _F (forward voltage) through it, which must be subtracted from the battery voltage E to determine the magnitude of the electric current flows through the same formula as in the schematic.

A great advantage of LED light emitting diodes is that the relatively small amount of electrical power require to "light" can be connected directly to the output of a logic circuit to indicate whether an output of "0 "or an output of" 1 . " There are two ways in which to perform the connection, referring to the following drawings:

In diagram (1) of the left, when the output of NAND is " 1 " actually this component will be putting a voltage of something like a +5 volts directly to the input LED, and as the other end of the LED is connected through resistance R level " 0 " or "electrical ground (GND) will be polarized just the right way" on "indicating the presence of" 1 "logical NAND output. resistance R is used to prevent a "short circuit" electrical and limit the magnitude of the current just what is required in order to power LED properly. And if the output of NAND is " 0 " actually this feature will not be getting any voltage to its output is zero volts, so that both ends of the LED is connected to "ground" with which the LED is off, indicating the presence of a " 0 " logical. With respect to the diagram (2) on the right, when the output of NAND is " 1 " will be putting a voltage of +5 volts at a terminal of the LED, and like the other LED terminal is also connected to the same voltage of +5 volts the LED will not conduct any electrical current is off, because in order to "ignite" the LED must have its anode connected to a " 1 " logical and its cathode connected to a " 0 " logical for the electric current can flow in the direction indicated by the arrow of the symbol, you can not turn to the two terminals connected to a " 1 "logical. On the other hand, when the output of NAND is a " 0 " Of course, this polarizes the LED in the right way and the electric current can flow from " 1 " a " 0 " coming through the output terminal NAND. (There is no contradiction in that the output terminal of NAND act as both an electrical input, because one thing is voltage of zero volts as the output and another thing is electrical current can enter through its output terminal, always remember that the "zeros" and "ones" are defined according to the presence or the absence of a voltage.) The main difference between the circuit (1) of the left and the circuit (2) on the right is that the left circuit LED lights when the output of NAND is " 1 "and turns off when the output of the LED is" 0 ", while the right circuit turns off the LED when the output of NAND is" 1 "and lights up when the output of NAND is" 0 . "

Possibly one of the most useful applications that may have an LED light emitting diode for the technician to maintain digital systems on the construction of the fundamental tool used by those technicians: the logic probe ( logic probe ), as follows:

Such probes generally have two light-emitting diodes LEDs, one to indicate a logic condition "0 (LOW or LO) and the other to indicate a logic condition "1 (HIGH or HI ). Generally do not require any internal power source (batteries), and taking their energy directly from the same circuit that is being analyzed through a terminal type "alligator" ( alligator clips). In the probe shown above, the alligator red terminal connects to the positive (+) power source, while a black alligator terminal is connected to the negative (-) from the source. The switch in this probe identified as "TTL / CMOS" is to choose appropriate levels of voltage and current as the logic family to which belongs the component being analyzed either TTL or CMOS (see Supplement # 1: logic families).

While in the hands of a skilled technician logic probe shown above serves admirably for the analysis, diagnosis and repair of the vast majority of digital systems in commercial use today, for certain highly specialized applications where the budget is not There is no problem other probes much more refined than they are actually logical probes in name only, since its complexity is really measuring instruments high accuracy as the "logic probe" LogicDart Hewlett-Packard:

Perhaps the most interesting thing is that the construction of the "logic probe" LogicDart used for the maintenance of digital systems based ultimately on the three logical functions basic integrated circuits used ultimately also based on the three basic logic functions.