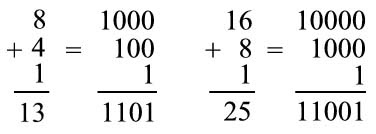This is the material that forms part of a book I wrote with the title Fundamentals Digital Logic: Problems and Solutions . The book's rights in Mexico are registered with the Directorate General of Copyright under the Registration Number 09031981-005 Artwork with entry number 04289 numbered.
The book is being uploaded to the Internet, using the opening provided by Google and Blogger, so that these materials are available to all students, teachers, technicians and engineers from all English-speaking countries 24 hours Day mode permanent.
From the days when the book was written under the meteor technological advances there have been many things have changed. For one thing, the cost of individual transistors and diodes are required for the construction of something as basic as the binary adder made it almost mandatory to study techniques such as Karnaugh map to minimize the number of discrete components required which in a project which required hundreds if not thousands of these components represents significant savings. Today, with large-scale integration, the savings you can expect to get with a minimization of some 28 components about 22 components are minimal. The simplification of the required logic is no longer a priority, even in small projects it is desirable to reduce the space required for interconnection wiring. But this is not the only thing that has changed. Previously, once a system was being designed logic circuits, the only way to be absolutely sure about the operation of the components specified in the design was to build a prototype in a laboratory. Today, these buildings are obsolete, we can "build" the system in a simulated through specialized programs that can run on a desktop computer. Although nothing replaces the experience of going to a lab and start connecting power supplies, interface components, and apply energy to see how the building works, the power of simulation programs can predict whether the designed system will work as expected or if the design will fail for some detail overlooked. You no longer need to apply solder to connect and remove the solder to disconnect, simply press today only a few keys to "turn off" and return to "connect" anything on the computer monitor.
However, there are some things that have not changed, which probably will not change. Those things are the fundamental principles on which digital logic rests which are designed and built in pocket calculators, electronic clocks without mechanical components, medical systems to determine the blood pressure automatically, in short, everything which is beating in digital logic. It is these principles that the book was intended initially. And the same principles that are still running today.
In the United States, by act of law, the February 17, 2009 comes into force an ordinance which mandates the replacement of all traditional television signals to digital signals. The whole world up to a future as fully digitized, and the essential knowledge digital logic has grown from a sophisticated art for highly skilled technicians, high-wage to a real need for many whose lives are being changed dramatically by the information revolution that is itself the product of the increasing sophistication of digital circuits .
An innovation in publishing this book on the Internet is the addition of numerous references to websites where the reader can find more information about various topics. Previously, the only way to get more data on a particular topic was referring to a good library (something difficult in most countries speaking, taking into account the high cost of technical books and the financial constraints faced by the vast majority of public libraries in these countries) or purchase technical books containing the information sought, which was not a good option for people with low estimates limited or hard to obtain the desired books in their own countries, having to order such books abroad through a distributor with long waiting times are common in these cases. In the new era of Internet, it has come to an end, and the whole world has become a giant electronic library which shared expertise are no longer the exclusive property of the high income nations.
Placing the book on the Internet has been a considerable effort, because it has essentially required to write the book from the beginning, which has consumed an enormous amount of time. Other problems have required having to take into account the limited capacity of some operating systems and browsers to "print" on the screen of the monitor certain special typefaces are not universal. A primary example of this is the logical inversion operation which is represented so that a logical variable that has undergone a process of investment is represented by a horizontal line placed above the letter representing the variable being "denied", which allows you to write expressions such as Boolean algebra:
However, not all possible combinations of operating systems and Internet browsers have typographic technology sophisticated enough to allow writing on the screen of the monitor this type of symbology (horizontal lines placed above the letters), which has caused much of what is published on the internet related in some way with Boolean logic does not resort to the use of upper rod to denote variables or negated expressions. To solve this and help readers to be able to read everything related in some way with Boolean algebra and logic circuits that exclude the use of upper rod limited the use of apostrophes, in various parts of the book also to get a line above the letters that can be displayed by the latest combinations of operating systems and browsers, are also represented separately in various parts of the book expressions with variables "denied" with a different color, the color blue (the color is assistance from the author to his readers, not a convention that is followed universally), this also putting an apostrophe as an alternative typeface immediately after the letter that is being "denied" according to an accepted practice in many texts to denote the "logical negation" with apostrophes. Thus, the above expression will be represented here in its equivalent form as follows:
A + A '= 1
When they appear in this book in Internet terms with this type of notation (using apostrophes) , will be placed in square brackets immediately after the words appearing in a previous line complemented with a horizontal bar above, this in order to indicate that it is completely expressions equivalent but different typeface so represented. Below is an example of this:
A + B = A · B
[ __ (A + B) ' = A' · B ' __]
[ __ (A + B) ' = A' · B ' __]
Here, the expression on the first line is equal to the expression in the second line. Both are completely equivalent.
Another problem inherent in the online publication of the book is that, unlike text form in which it can put many small details that still can be distinguished visually, many of these fine details can be easily lost in a color SVGA monitor because the vast majority of computer monitors has limited resolution capability. This can only be offset by the diagrams and figures larger. Unfortunately, to make the greatest figure, the host site (in this case, Blogger) automatically activates an attribute known as the "image resizing" which "compresses" the image size so that it can fit within the area visual page. Fortunately, the image original is not discarded, but can be obtained by merely "click" with the mouse within the image. In those cases in which it is highly desirable to carry out here the extension of the image in order to retrieve some visual data are lost during the compression process, the reader will recommend expanding the image with text green letter that tells you zoom . Here's an example that illustrates this point, which shows a basic computer built around the Zilog Z80 microprocessor:
If the reader attempts to obtain more details on this circuit, it may not succeed. However, if you click with the mouse within the image, Blogger will send a larger image. And if the reader does it again click with the mouse within the image, possibly get an extension even more (this depends on the browser being used, the size of monitor being used, and even the operating system). There is also an option in most modern browsers can open a separate window and independent to activate a link, which allows you to perform the zoom operation showing the enlarged image in a separate window, allowing easily switch between text and image.
is important to note that although not all images tells the reader to perform the procedure zoom, many of them can be seen with better resolution and clarity when performing the procedure.
There is another reason for carrying out the process of "image magnification. One advantage of online publications is that they allow something that simply is not possible in a printed text, including files animated gif format , which can sometimes highlight so impressive to a point of importance, which makes them a excellent teaching aid. The vast majority of these files animated gif , to be included within the pages of Blogger, do not show any animation, because it allows the page content. For example, the following cartoon may be displayed or not a completely static picture when seen within this page depending on the browser you are using (Mozilla Firefox, Internet Explorer, Google Chrome, Opera, etc.)
Also the next drawing is actually a cartoon may appear as a completely static image:
But if carried out the process of zoom in on each of the last two pictures, then to be abandoned temporarily to load each page file gif can witness the full animation, after which they can return to this page as it is customary in all browsers.
This work is to be released to the Web a few years ago was initially optimized for a 17 "monitor with a screen resolution of 1024x768 pixels, which became the de facto standard for older monitors the type of tube ray cathode ray (CRT) to display an image with an "aspect ratio" ( aspect ratio) of "four to three," or 4:3, this being the reason for the width of an image (measured horizontally) to their height (measured vertically). Soon appeared flat screen monitors, initially quite expensive, the cost came down to be replacing a lot of older monitors the type of cathode ray tube. These flat panel monitors allow a panoramic presentation of much greater width with which it would be possible to put large images in their original size without requiring the reader to zoom . However, is not possible to redo the work to maximize the availability of widescreen flat for the simple reason that in many English-speaking countries with limited budgets still depend on older monitors, and even if they do change to modern screen monitors flat bulk is likely to continue to use many of these computers, "oldies" to which are connected to retain older operating systems (Windows XP, Windows Millennium, etc.) do not guarantee that updates the capacity to absorb the flat-screen functionality. This addition to the submission of logs is not wide format guaranteed to all browsers used today. Thus, more for reasons of compatibility with the wide variety of systems used today in the English-speaking countries for reasons of taste, the work has been left intact as it first appeared.
Given the vast superiority of the Mozilla browser on the Internet Explorer browser, if there are problems for proper viewing of all materials contained in this book is strongly recommended to install Mozilla on the machine where these materials will be consulted, which does not produce conflicts with browsers already on the machine itself and instead give a verified top choice for this text.
is important to note that this author has spared no resources to include as many diagrams, on the educational provision of visual education is much more effective and more durable than merely symbolic teaching. Moreover, exploiting the fact that almost all monitors now used to connect to the Internet under almost any operating system are color monitor capable of displaying a wide range of bright colors, a large number of drawings of the book have added colorful generously to make the presentation more attractive to maintain focus and achieve the reader's attention, unlike the papers submitted for publication in professional journals in which customary to "seriousness" of the materials accepted for publication not only by reducing to an absolute minimum possible number of drawings and illustrative examples, but doing it all black and white, like a solemn mourning session.
Each of the issues resolved included in the book has a very specific educational purposes, either to introduce or expand a new idea, or provide some practice in a key concept, plus they are arranged in increasing order of difficulty , going from easiest to most difficult, which is why it is important to study them in the order they are posted. In several parts of the book, you incur details that may seem redundant to an extent that may seem almost ridiculous, as is the case with several problems related to Boolean algebra, where several parties will see an additional set of steps resolution that would possibly be eliminated by most book publishers, and certainly would not be admissible in a professional journal. However, the intention of this work is to make it accessible to the broadest audience possible, which includes people not necessarily be studying for a university degree and that even these materials will be studying self-taught, self-employed, without the benefit of the assistance of a competent teacher at his side who can be clarifying their doubts, why it was necessary to go into detail on things that otherwise should be very clear way for people with university degrees.
A great advantage of publishing a book on the Internet in contrast with the publication of the traditional paper book is the author of the book may receive requests from his readers (teachers, students, general public) requesting that a subject is discussed in more detail, clarity, or with better examples and visual aids. The author of this book is in happy to answer your readers anything that will broaden and enhance the educational value of this work. On the other hand, misspellings, typographical and human plan can be communicated to the author and can be corrected almost instantly, something not possible in the print edition of a book that barely and sporadically published a "misprint." The author of this book, readers appreciate the marking of any such error promising a prompt correction of it in as your time permits, as well as appreciate the remark of "dead links" of the Internet referred to in this work with to remove and possibly substitutes to replace them with alternates. This makes a book published online in a work "alive", unlike a printed book that is unable to interact with their readers. Finally, the best advantage of all is that the publication of a book on the internet not having to go through the sad process of review by the editors of the book, which in many cases mutilated and change both the original text at the end of the text published very little resembles the original intention of the author.
As another sign of the times, this "second edition" of the book is something that appeared in the original edition: the addresses of various Internet sites which can be downloaded (download) executable programs, most of them free, to assist students and technicians in the study, analysis and design of logic circuits.
For the book's publication on the Internet, have also included several supplements that were not part of the original work, starting with Supplement # 1 dealing in more detail on the families of electronic components which are implemented basic logic functions. The Supplement # 1 something must satisfy the curiosity of those who want to know what is going more deeply into those "black boxes" we have symbolized as basic logic functions or derivatives thereof. Although a technician who knows the basics of digital logic can not spread it very well without knowing what's inside those black boxes, and may be able not only to repair systems that use digital logic, but even up to make designs as a professional in many there is always curious about what is happening "inside." The exhibition's theme of logic families is presented in a qualitative, not quantitative way, since the latter would require us to go more in depth on issues such as the operation of bipolar transistors and effect transistors field Kirchofff laws, thermal effects, etc., and this book assumes that the average reader of this book introductory to the subject has no such knowledge. We also have the Supplement # 2 which is sovereign the pinnacle of the integration of basic logic functions on a large scale: the microprocessor, followed by Supplement # 3 describing how he works the microprocessor and Supplement # 4 is in fact a charge divided into two parts that have some relationship: the Supplement 4a: The 8086 microprocessor instructions and Supplement 4b: Microprocessor Programming that describes how it is out the development of programs for them to be executed by a microcomputer. There is no better way to get an idea on how to carry out the programming of a microprocessor to have seen a set of instructions of a typical microprocessor, and Intel 8086 microprocessor for its relative simplicity offers a good starting point for this. In addition to these supplements, we Supplement # 5 that describes how a microcomputer can communicate with the outside world when there is only one channel (or electrical cables) through which to transmit information. In addition to the supplements already mentioned, we have attached two supplements described as certain basic analog integrated circuits (as opposed to integrated circuits digital discussed in the book) often used in systems that often appear hybrids in which the design requires the integration of both digital electronics components such as analog electronics. These are the Supplement # 6 dealing with the operational amplifier better known as op-amp , and Supplement # 7 dealing with the timer 555, better known as 555 timer.
response to a request by a considerable amount of my readers who feel somewhat my fellow students or teachers, I have added an additional last minute, the Supplement # 8 that provides an introduction to ladder diagrams and the application of these diagrams in the programming of programmable logic controllers. This can be seen in some ways the point of entry into the areas of industrial automation, most notably the robotics or mechatronics .
For those college students who want to find in this book some information about the representation of sequential logic circuits using the theoretical model and the Moore machine model Mealy machine theorist, has included the Supplement # 9 with a brief discussion on these topics.
addition to the many numerous figures and diagrams which consists of original work, have been added in the figures and diagrams book freely available on the Internet to further enhance the clarity of the text. This profusion of images should serve as a substitute for the lack of a board with which the author of this book make clear to students normally issues a little more difficult to grasp. It has made every effort to keep the original spirit of the book, making changes only when it is a better explanation or adding more pictures and diagrams.
To save time and to have all the chapters of this book available that has an almost immediate, convenient and efficient alternative for those students or educational institutions with Internet connections is to go slow speed " keeping "in the computer hard disk (or a memory such as" flash drive USB) per page (complete) that is posted each chapter as you go down the materials. This is always possible in most modern browsers like Internet Explorer or Mozilla with the option of the menu line set to "File" (File) with an option to "Save Page Ace .." (Save the page as ...). Thus, the next time you need to refer to a chapter, rather than access the web page down slowly all the materials can directly access the page from the same hard disk or from memory "flash drive" (any mode Internet connection required to download additional content provided by Blogger to build the page) at a much faster, making this work in an "electronic book" in the fullest sense of the word.
Added an updated bibliography that can be used as reference material and documentation. It may be of interest to many readers to know that some of the books in literature can be downloaded free from the Internet to one or more sites. Libero
since this book with the hope that their materials and lessons can be of any use to those wishing to learn more about what are the essential foundations on which they are based computers that make it possible to extend the same to everyone Internet.
The Author
Armando Martinez Tellez